Aufgabe 8
Gegeben sind die Funktionsgleichungen f(x)= x²(x+2)² und g(x)=x(x+2)
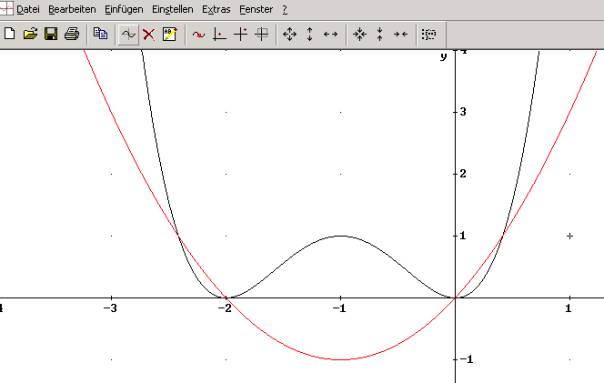
a) Zeichne die Graphen der Funktionen.
b) Untersuche die Funktionen f und g auf charakteristische Punkte.
c) Berechne das Flächenmaß, der von den Graphen von f und g gebildeten Fläche.
d) Zeige rechnerisch, dass die Funktionsgraphen von f und g symmetrisch sind.
Tipps
Zu 8. Um schneller mit den Funktionen arbeiten zu können, definieren wir sie durch:
f(x):= x²(x+2)² und durch g(x):=x(x+2)
Wir können dann mit f(x) und g(x) rechnen, ohne die Terme zu benutzen. Z.B. liefert dif(f(x),x) die Ableitung f´(x) und solve(f(x)=g(x),x) die Schnittstellen der beiden Funktionen.
 Um
die Funktionsgraphen zu zeichnen, markiert man sie, so dass sie blau unterlegt
sind und wählt das Zeichen
Um
die Funktionsgraphen zu zeichnen, markiert man sie, so dass sie blau unterlegt
sind und wählt das Zeichen

 Dadurch
wechselt man ins 2D-Graphik-Fenster und erhält durch Klick auf die gewünschten Graphen.
Dadurch
wechselt man ins 2D-Graphik-Fenster und erhält durch Klick auf die gewünschten Graphen.
![]()
![]()
![]()
![]()
 Der
Bildausschnitt kann durch Zoomen verändert
Der
Bildausschnitt kann durch Zoomen verändert
![]() oder
unter Einstellen angepasst werden.
oder
unter Einstellen angepasst werden.


Unter Extras können weitere Formatierungen z.B. Graphenfarbe vorgenommen werden.
Zurück zum Algebrafester gelangt man durch Klick auf
Man kann auch gleichzeitig das Algebra- und das Graphikfenster öffnen.
![]() Fenster
und anschließend Vertikal anordnen liefert eine Zweiteilung des
Bildschirms.
Fenster
und anschließend Vertikal anordnen liefert eine Zweiteilung des
Bildschirms.
![]()
Die Kurvenuntersuchung verläuft wie im herkömmlichen Unterricht. Lediglich das hinreichende Kriterium kann vernachlässigt werden, da die Existenz der Extrem- bzw. Wendestellen durch den Graphen gesichert werden kann.
Versuchen Sie es selbst , klicken Sie dazu auf eigener Versuch und schließen
Sie anschließend das Derivefenster.