| |
|
|
| |
|
Der Fachbereich Mathematik und |
|
Die Wirtschafts- und Sozialwissenschaftliche
Fakultät |
|
|

|
|
Tag der Optimierung,
Mittwoch, 12. Juni 2002,
Hörsaal E28, Mathematikgebäude
|
Vortrag (17.00 bis 18.00 Uhr):
Prof. Dr. Stephan Dempe (Technische Universität
Bergakademie Freiberg):
Optimalitätsbedingungen für
Zwei-Ebenen-Optimierungsaufgaben
Abstract:
Zwei-Ebenen-Optimierungsaufgaben sind hierarchische Optimierungsprobleme,
bei denen die Menge zulässiger Punkte des sogenannten Problems der
oberen Ebene von der Menge der optimalen Lösungen des Problems der
unteren Ebene abhängt. Zu seiner Definition sei das folgende parametrische
Optimierungsproblem betrachtet:
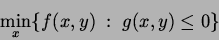 | (Problem der unteren Ebene) |
Die Optimalmenge dieses Problems sei mit
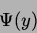 bezeichnet. Dann besteht die Zwei-Ebenen-Optimierungsaufgabe in
bezeichnet. Dann besteht die Zwei-Ebenen-Optimierungsaufgabe in
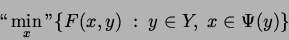 | (Problem der oberen Ebene) |
Zwei-Ebenen-Optimierungsaufgaben haben viele Anwendungen wie zum Beispiel die
Prinzipal-Agenten-Theorie in der Ökonomie und die Suche nach besten chemischen
Gleichgewichten.
Die Anführungszeichen in der obigen Definition sind verwendet worden, um die
Unbestimmtheit in dieser Definition auszudrücken im Falle, dass das Problem
der unteren Ebene keine eindeutige optimale Lösung besitzt. Die sich daraus
ergebenden Konsequenzen und möglichen Modifikationen des Problems (der
optimistische und der pessimistische Zugang) werden gemeinsam mit den entsprechenden
Optimalitätsdefinitionen Gegenstand des Vortrags sein.
Das Hauptziel des Vortrags besteht in der Formulierung von notwendigen und
hinreichenden Optimalitätsbedingungen in beiden Zugägen. Unter Verwendung
bestimmter Voraussetzungen wird es sich zum Beispiel erweisen, dass es eine
notwendige Voraussetzung für ein lokales Optimum ist, dass eine gewisse Anzahl
von Ungleichungssystemen keine Lösung besitzt. Das ist ein wesentlicher
Unterschied zu Ein-Ebenen-Optimierungsaufgaben, wo die Unlösbarkeit lediglich
eines Ungleichungssystems aus der lokalen Optimalität eines Punktes folgt.
Homepage: Prof. Dr. S. Dempe
Email: dempe@math.tu-freiberg.de
Zurück zur Übersicht


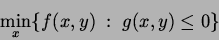
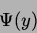 bezeichnet. Dann besteht die Zwei-Ebenen-Optimierungsaufgabe in
bezeichnet. Dann besteht die Zwei-Ebenen-Optimierungsaufgabe in