Der Fachbereich Mathematik und
Die Wirtschafts- und Sozialwissenschaftliche Fakultät

Tag der Optimierung, Mittwoch, 12. Juni 2002, Hörsaal E28, Mathematikgebäude

Vortrag (14.30 bis 15.30 Uhr):

Prof. Dr. Diethard Pallaschke (Universität Karlsruhe):

Morse-Theorie für stückweise differenzierbare Funktionen
auf differenzierbaren Mannigfaltigkeiten

Abstract: Ausgangspunkt einer Morse-Theorie für stückweise differenzierbare Funktionen ist die folgende Verallgemeinerung des zweiten Morse-Lemmas von H. Th. Jongen. Danach sind stückweise differenzierbare Funktionen in einer Umgebung eines regulären Punktes linearisierbar, und nach Einführung neuer Koordinaten können die Variablen so zerlegt werden, daß eine stückweise differenzierbare Funktion 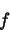     in einer Umgebung eines nichtdegenerierten kritischen Punktes 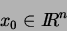     topologisch äquivalent zu einer Funktion der Form

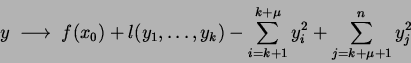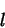ist. Dabei ist      eine stetige, stückweise lineare Funktion, die sich als max-min Kombination aus den Koordinaten-Funktionen      und 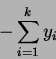     zusammensetzt. In dieser Darstellung entspricht der zweite Summand dem differenzierbaren Anteil der Funktion, während der erste Summand den nicht-differenzierbaren Anteil der Funktion wiederspiegelt.
Aus dem zweiten Morse-Lemma folgt nun, daß die Niveaumengen von stückweise differenzierbaren Funktionen auf differenzierbaren Mannigfaltigkeiten homotopie-äquivalent zum Join zwischen dem differenzierbaren und nicht-differenzierbaren Anteil der Niveaumengen sind. Mit Hilfe der Künneth-Formel läßt sich dann der Morse-Index über die relativen Homotopiegruppen der Niveaumengen bestimmen, so daß insgesamt die klassische Morse-Theorie bis zu den Morse-Ungleichungen vollständig für stückweise differenzierbare Funktionen auf differenzierbaren Mannigfaltigkeiten übertragen werden kann.

Homepage: Prof. Dr. D. Pallaschke
Email: lh09@rz.uni-karlsruhe.de

Zurück zur Übersicht