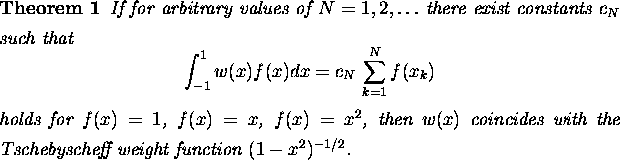
Even in the univariate case there are only a few quadrature formulae with equal weights. These are quadrature formulae for the weighted integral with the weight function of the Tschebyscheff-polynomials of the first kind or for low degrees formulae for integrals with a constant weight function. More exactly we have the following theorems (see e. g. Krylov [13]).
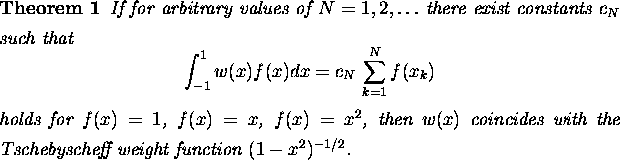
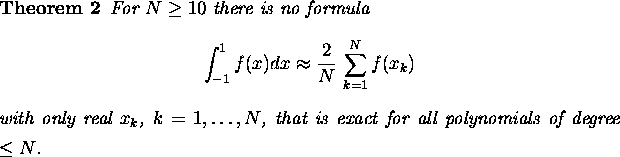
The univariate results show that the existence of quadrature formulae with equal weights cannot be expected too often in the far more complicated multivariate case. Results of the theory of spherical designs and multivariate Gauss quadrature formulae confirm this conjecture [1, 2, 3].