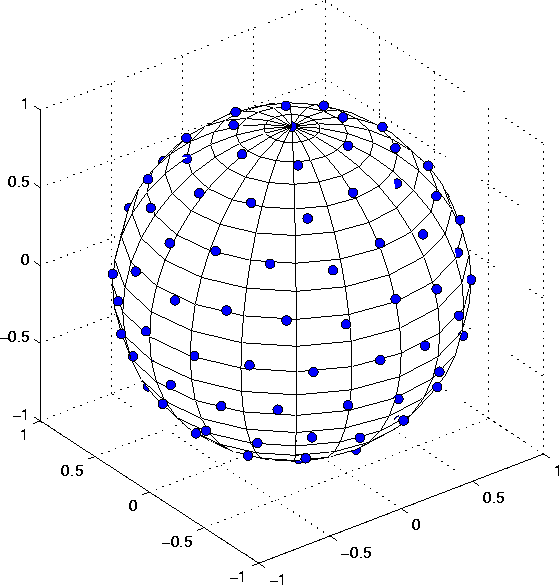

All these formulae use a number of nodes on the sphere at which the function is evaluated. The function values are then multiplied with certain weights and the results are summed up. We were able to compute nodes and weights such the integration error drops to $10^{-12}$ for many functions.
If you want to look at the details of the underlying theory you can download the accompanying technical report as a ps-file (1133K) or it's abstract. See also my other publications. A (sligthly broken) html-version of the report can be found here.
The following files contain the node coordinates and the corresponding weights in the following syntax: each line of the file contains four numbers, the three cartesian coordinates of a node, then the weight for this node. There are as many lines in the file as there are nodes in the integration formulae. Thus, the first column of the file contains all the first coordinates of the nodes, while the last column of each file contains all the weights of the integration formulae.
You can download integration formulae for the following node numbers:
4 ,
9 ,
16 ,
25 ,
36 ,
49 ,
64 ,
81 ,
100 ,
121 ,
144 ,
169 ,
196 ,
225 ,
256 ,
289 ,
324 ,
361 ,
400 ,
441 ,
484 ,
529 ,
576 ,
625 ,
676 ,
729 ,
784 ,
841 and
900
Wonder about these strange numbers? Please read the technical report.
Please note that we have normalized the coordinate system such that the first node in the file has coordinates (0, 0, 1). This may be done without loss of generality, but you may of course employ arbitrary rotations to change the node systems.