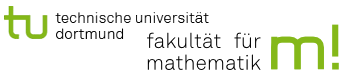1. Produktregel.
2. $x$ mit höchstem Exponenten ausklammern, mehrfach l'Hospital anweden.

1. Nullstellen:
   $f(x)=0 \LR x=3 \lor x=0$
   Extrema: $ f'(x)=(x^3-6x)e^x\\ f''(x)=(x^3+3x^2-6x-6)e^x\\ f'(x)=0 \LR x=0 \lor x=\pm \sqrt 6\\ f''(0)=-6 \RA \text{rel. Max: } (0,0)\\ f''(-\sqrt 6)= %(-6\sqrt 6 + 18 + 6\sqrt 6 -6)e^{-\sqrt 6}= 12e^{-\sqrt 6}>0 \RA \text{rel. Min: } (-\sqrt 6,-6(\sqrt 6+3)e^{-\sqrt 6})\\ f''(\sqrt 6)= %(6\sqrt 6 + 18 - 6\sqrt 6 -6)e^{-\sqrt 6}= 12e^{\sqrt 6}>0 \RA \text{rel. Min: } (\sqrt 6,6(\sqrt 6-3)e^{\sqrt 6}) $
2. Da $\D \lim_{x\to\infty} \left(x^3-3x^2\right)=\lim_{x\to\infty} x^3\left(1-\frac 3x\right)=\infty$ und $\D \lim_{x\to\infty} e^x=\infty$
   $\D \RA \lim_{x\to\infty} f(x)=\infty$.
   $\D \lim_{x\to-\infty} f(x)=\lim_{x\to-\infty}\frac{x^3-3x^2}{e^{-x}}\stackrel{\text{l'H.}}{=}\lim_{x\to-\infty}\frac{3x^2-6x}{-e^{-x}}\stackrel{\text{l'H.}}{=} \lim_{x\to-\infty}\frac{6x-6}{e^{-x}}\stackrel{\text{l'H.}}{=}\lim_{x\to-\infty}\frac{6}{-e^{-x}}=0$

Quotienten- oder Kettenregel, Periodizität beachten.

$\D f'(x)=\frac{\sin x-\cos x}{\left(2+\sin x+\cos x\right)^2}$

Da die Ableitung eine Komposition stetiger Funktionen ist, und ihr Nenner ungleich Null ist,
ist auch die Ableitung stetig.

$\D\RA f'(x)\stackrel{!}{=}0\LR \sin x\stackrel{!}{=}\cos x\RA x=\frac\pi 4+n\pi,\quad n\in\mathbb{Z}$

Vergleich der Funktionswerte zur bestimmung der Extrema:

$\D f(\frac\pi 4+n\pi)=\frac{1}{2+\sin(\frac\pi 4+n\pi)+\cos(\frac\pi 4+n\pi)}=\frac{1}{2\left(1+\sin(\frac\pi 4+n\pi)\right)}\\ \D=\begin{cases} \frac{1}{2+\sqrt 2},\quad n\text{ gerade}\RA\text{ Minima bei }x=\frac\pi 4+2n\pi\\ \frac{1}{2-\sqrt 2},\quad n\text{ ungerade}\RA\text{ Maxima bei }x=-\frac{3\pi}{4}+2n\pi \end{cases}$

Aus der Stetigkeit von $f(x)$ und $f'(x)$ und den ermittelten Extrema folgt:

$\D f(x)\text{ ist} \begin{cases} \text{streng monoton fallend auf }\D\left[-\frac{3\pi}{4}+2k\pi,\frac{\pi}{4}+2k\pi\right]\\ \text{streng monoton steigend auf }\D\left[\frac{\pi}{4}+2k\pi,\frac{5\pi}{4}+2k\pi\right] \end{cases} k\in\mathbb{Z}$

1. Kettenregel.
2. $x=e^{\ln x}$, Kettenregel.
3. Quotientenregel.

1. $ \D f'(x)=\frac 12 \left(1+x^2\right)^{-\frac 12}\cdot 2x=x\left(1+x^2\right)^{-\frac 12}\\ \D f''(x)=\left(1+x^2\right)^{-\frac 12}-\frac 12\left(1+x^2\right)^{-\frac 32}\cdot 2x\cdot x=\left(1+x^2\right)^{-\frac 32}\left[1+x^2-x^2\right]\\ \D=\frac{1}{\sqrt{1+x^2}^3} $


2. $ \D\left(\sin{x}\right)^{\sin{x}}=e^{\sin{x}\ln\sin{x}}\\ \D f'(x)=e^{\sin{x}\ln\sin{x}}\left( \cos{x}\ln\sin{x} + \sin{x}\frac{\cos{x}}{\sin{x}}\right)\\ \D=\left(\sin{x}\right)^{\sin{x}}\cos{x}\left(1+\ln\sin{x}\right) $


3. $ \D f'(x)=\frac{\cos x\left(2+\cos x\right)-\sin x\left(-\sin x\right)}{\left(2+\cos x\right)^2}=\frac{2\cos x +\cos^2 x+\sin^2 x}{\left(2+\cos x\right)^2}=\frac{2\cos x+1}{\left(2+\cos x\right)^2}\\ \D f'(x)\stackrel{!}{=}0\LR\cos x=-\frac 12\LR x=\frac 23 \pi\lor x=\frac 43 \pi $

Tipp...

1. $\D M\subset\mathbb{R}\RA 1-x^2\geq 0\LR|x|\leq 1\RA D=[-1,1]$

2. Extremwerte bestimmen:

   $\D f'(x)=\frac{1-2x^2}{\sqrt{1-x^2}}\stackrel{!}{=}0\LR x=\pm\frac{1}{\sqrt{2}}\\ f\left(\pm\frac{1}{\sqrt{2}}\right)=\pm\frac 12\RA\text{ Max/Min bei} \left(\pm\frac{1}{\sqrt{2}},\pm\frac 12\right)$

   Randwerte überprüfen:

   $ f(\pm 1)=0\\ \RA M=\left[-\frac 12,\frac 12\right]$

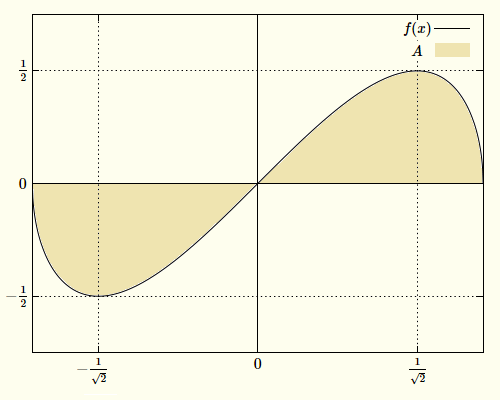
4. Zwischen $x=0$ und $x=\frac{1}{\sqrt 2}$ ist die Funktion streng monoton wachsend $\RA$ bijektiv, also existiert eine Umkehrabbildung.
5. $g'(f(\frac{1}{2}))=\frac{1}{2}$.
6. Da $-f(x)=f(-x)$ ist $\int_{-1}^1 f(x) dx=0$ Um die Fläche zu berechenen kann in diesem Fall $2\cdot\int_0^1 f(x) dx$ ausgewertet werden: $ \D 2\int_0^1 x\sqrt{1-x^2} dx,\qquad \text{Substitution: }u=1-x^2,\quad dx=-\frac{du}{2x}\\ \D 2\int_1^0 x\sqrt{u}\left(-\frac{du}{2x}\right)=-\int_1^0\sqrt{u}\ du=-\left[\frac 23 \sqrt{u}^3\right]_1^0=\frac 23 $