Aufgabe 1
Seien die Funktionen $\D f: [-\pi, \pi] \rightarrow \bbbr,\,
f(x) =
\begin{cases}
\D 0, & x \in \Big[-\pi, \D -\frac{\pi}{3}\Big) \\
\D 1, & x \in \Big[\D -\frac{\pi}{3}, 0\Big] \\
\D 0, & x \in \Big( 0, \pi \Big]
\end{cases}$ und
$g: [-\pi, \pi] \rightarrow$
$g(x) =
\begin{cases}
\D 0, & x \in \Big[-\pi,0 \Big) \\
\D 1, & x \in \Big[0, \D \frac{\pi}{3} \Big] \\
\D 0, & x \in \Big( \D \frac{\pi}{3}, \pi \Big]
\end{cases}$
- Berechenn Sie die Faltung $h = f \ast g$
- Berechnen Sie die komplexen Fourierkoeffizienten von $f, g$ und $h$.
Hinweis: die Ergebnisse müssen nicht in Real- und Imaginärteil aufgespalten werden.
Tipp
- Die Faltung ist definiert durch: $\D (f \ast g)(x) := \int_{-\infty}^{\infty}\,f(x-t)\,g(t)\,dt.$
- Die Berechnung der komplexen Fourierkoeffizienten $c_n$
einer $2\pi$-periodischen Funktion $f$ erfolgt über:
$\D c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) e^{-inx}\,dx$
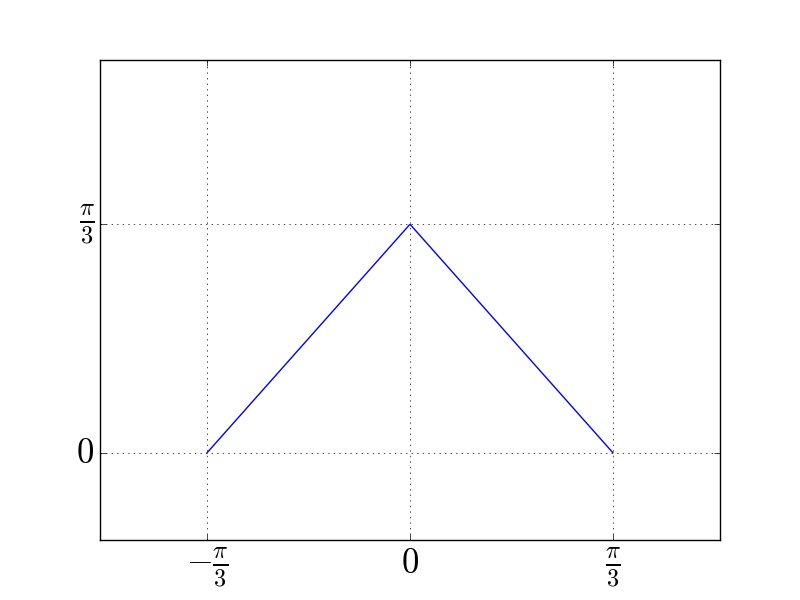
Skizze der Faltung $h$:
(Klicken zum Vergrößern)
Lösung
Aufgabenteil 1:
Die Faltung $h = f \ast g$ lautet:
$h(t) = (f \ast g)(t) = \D \int_{-\pi}^{\pi} f(t) g(x-t)\,dx$
Es müssen vier Intervalle unterschieden werden:
$\begin{align}
-\pi \le &t \le - \frac{\pi}{3}\,&:\;&h(t) = 0 \\
\frac{\pi}{3} \le &t \le \pi \,&:\;&h(t) = 0 \\
0 \le &t \le \frac{\pi}{3}\,&:\;&h(t) = \frac{\pi}{3} - t \\
-\frac{\pi}{3} \le &t \le 0\,&:\;&h(t) = t + \frac{\pi}{3}
\end{align}$
Aufgabenteil 2:
Für $f$ und die Koeffizienten $c_k$ gilt:
$\begin{align}
f:\,c_k
&= \D \frac{1}{2\pi} \int_{-\frac{\pi}{3}}^0 e^{-ikx}\,dx = \frac{1}{2\pi} \frac{1}{-ik} e^{ikx} \Bigg|_{-\frac{\pi}{3}}^0 \\
&= \frac{i}{2\pi k} (1- e^{ik \frac{\pi}{3}}) \\
\\
\text{und } c_0 &= \frac{\pi}{3} \frac{1}{2\pi} = \frac{1}{6}
\end{align}$
Die Koeffizienten $d_0$ von $g$ lauten:
$\begin{align}
g:\,d_k
&= \frac{1}{2\pi} \D \int_0^{-\frac{\pi}{3}} e^{-i k x}\, dx = \frac{1}{2\pi} \D \frac{1}{-i k} e^{-i k x} \D \Bigg|_0^{\frac{\pi}{3}} \\
&= \D \frac{i}{2 \pi k} (\D e^{ik -\frac{\pi}{3}} - 1 ) \\
\\
\text{und } d_0 &= \frac{1}{6}
\end{align}$
Die Koeffizienten $e_k$ von $h$ berechen sich wie folgt:
$\begin{align}
h:\,e_k
&= \frac{-2\pi}{(2\pi k)^2} \D (e^{-ik\frac{\pi}{3}} - 1 - 1 + e^{ik \frac{\pi}{3}}) \\
&= \frac{1}{2\pi k^2} (2 - e^{ik \frac{\pi}{3}} - e^{-ik \frac{\pi}{3}}) \\
&= \frac{1- \cos \frac{k\pi}{3}}{\pi k^2}
\\
e_0 &= 2\pi \frac{1}{6} \frac{1}{6} = \frac{\pi}{18}
\end{align}$
Skizze der Faltung $h$:

(Klicken zum Vergrößern)
Aufgabe 2
Sei $f: [-\pi, \pi] \rightarrow \bbbr$ gegeben durch
$f(x) =
\begin{cases}
\D \frac{\pi}{2}-|x|, & \D \frac{-\pi}{2} \le x \le \D \frac{\pi}{2} \\
\D 0, & \text{sonst} \\
\end{cases}$ und
- Skizzieren Sie $f$.
- Berechnen Sie die Koeffizienten $c_{-4}$ bis $c_{4}$ der komplexen Fourierreihe von $f$.
- Bestimmen Sie alle $n \in \mathbb{Z}$, so dass $c_n = 0$ ist.
Tipp
Da $f(x)$ eine gerade reellwertige Funktion ist, gilt: $\D \int_{-\pi}^{\pi} f(x) e^{-inx}\,dx = 2 \int_0^{\pi} f(x)\cos nx\,dx$.
Lösung
Aufgabenteil 1:
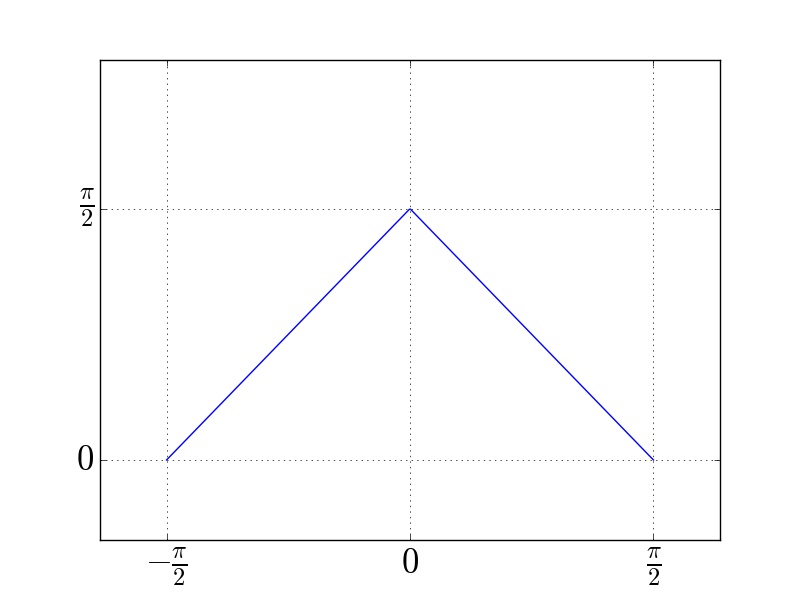
(Klicken zum Vergrößern)
Aufgabenteil 2:
Da ein $f$ eine gerade Funktion ist, sind die Fourierkoeffizienten $c_k$ reell.
$\D c_0=\frac{1}{2\pi}\int_{-\pi}^\pi f(x)\, dx=\frac{1}{\pi}\int_0^{\pi} (\frac{\pi}{2}-x)\, dx
=\frac{1}{\pi}(\frac{\pi}{2}x-\frac{x^2}{2})\Big|_0^{\pi/2}=\frac{\pi}{8}$
$\begin{align}
c_n &= \frac{1}{2\pi} \int_{-\pi}^\pi f(x) e^{-inx}\ dx\\
&= \frac{1}{\pi} \int_0^{\pi/2} (\frac{\pi}{2} - x) \cos nx\, dx \quad\text{da $f$ gerade ist }\\
&= \frac{1}{\pi}\Big[ \frac{\pi}{2n}\sin nx - \frac{x}{n} \sin nx - \frac{1}{n^2} \cos nx \Big]_0^{\pi/2} \\
&= \frac{1}{\pi}\Big(- \frac{1}{n^2} \cos n\frac{\pi}{2} +\frac{1}{n^2}\Big) \\
&=\frac{1}{\pi n^2}\left(1-\cos \frac{n\pi}{2}\right)
\end{align}$
Es ist $\D \cos \frac{n\pi}{2}=1$ für $n=0$ und $n=\pm 4$, $\D \cos \frac{n\pi}{2}=0$ für $n=\pm 1$ und $n=\pm 3$ und $\D \cos \frac{n\pi}{2}=-1$ für $n=\pm 2$.
Die Ergebnisse für $n=-4, -3, ... 3, 4$ lauten daher
$\begin{align}
c_{0} &= c_{-4} = c_4=0 \\
c_{1} &= c_{-1} = \frac{1}{\pi} \\
c_{2} &= c_{-2} = \frac{2}{4\pi}=\frac{1}{2\pi} \\
c_3 &= c_{-3} = \frac{1}{9\pi}
\end{align}$
Aufgabenteil 3:
$c_n=0\LR \cos \frac{k\pi}{2}=1\LR \frac{k\pi}{2}=2m\pi\LR k=4m$, $m\in \mathbb{Z}\setminus\{ 0 \}$
Aufgabe 3
Sei
$f(x) =
\begin{cases}
\D e^{-x}, & x > 0 \\
\D 0, & x \le 0 \\
\end{cases}$ und
- Berechen Sie $g = f \ast f$.
- Berechnen Sie die Fouriertransformierte $\mathcal{F}f(t)$.
- Berechen Sie $\mathcal{F}g(t)$ sowohl direkt wie auch mit dem Faltungssatz.
Tipp
- Die Faltung ist definiert durch: $\D (f \ast g)(x) := \int_{-\infty}^{\infty}\,f(x-t)\,g(t)\,dt.$
- Für die Fouriertransformierte $\hat{f}(t)$ gilt: $\D \hat{f}(t) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} f(x) e^{-i t x}\,dx$
- Der Faltungssatz lautet: $\D (\mathcal{F}(f \ast g)(x))(t) = \sqrt{2\pi}(\mathcal{F} f(x))(t) (\mathcal{F} g(x))(t)$
Lösung
Aufgabenteil 1:
$\begin{align}
(f \ast f)(x)
&= \int_0^{x} e^{-(x-t)}\,e^{-t}\,dt = \int_0^{x} e^{-x+t-t}\, dt \\
&= \int_0^{x} e^{-x}\,dt = e^{-x}\;t \Bigg|_0^x \\
&= x e^{-x}
\end{align}$
Aufgabenteil 2:
Für die Fouriertransformierte $\mathcal{F}f(t) = \hat{f}(t)$ gilt:
$\begin{align}
\hat{f}(t)
&= \D \frac{1}{\sqrt{2\pi}} \int_{0}^{\infty} e^{-x} e^{-i t x}\,dx \\
&= \D \frac{1}{\sqrt{2\pi}} \int_0^{\infty} e^{-x(1+it)}\,dx \\
&= \D - \frac{1}{\sqrt{2\pi} (1+it)} \; e^{-x(1+it)} \Bigg|_0^{\infty} = - \frac{1}{\sqrt{2\pi} (1+it)} (0-1) \\
\\
&= \D \frac{1}{\sqrt{2\pi}} \frac{1}{1+it}
\end{align}$
Aufgabenteil 3:
direkte Berechnung:
$\begin{align}
(\mathcal{F}(f \ast f)(x))(t)
&= \D \frac{1}{\sqrt{2\pi}} \int_{0}^{\infty} x e^{-x} e^{-i t x}\,dx = \frac{1}{\sqrt{2\pi}} \int_{0}^{\infty} x e^{-x(1+it)}\, dx \\
&= \D \frac{1}{\sqrt{2\pi}} \Big[- \frac{x}{1+it} e^{x(1+it)} \Big]_0^{\infty} + \frac{1}{\sqrt{2\pi}} \frac{1}{1+it} \int_{0}^{\infty} e^{-x(1+it)}\, dx\\
&= \frac{1}{\sqrt{2 \pi}} \D \Big[-\frac{x}{1+it} e^{-x(1+it)} - \frac{1}{(1+it)^2} e^{-x(1+it)} \Big]_0^{\infty} \\
&= \frac{1}{\sqrt{2\pi}} \frac{1}{(1+it)^2}
\end{align}$
Es wurde darauf verzichtet, das Einsetzen der Grenzen explizit darzustellen.
Anzumerken ist aber, dass für Grenzwerte der Form $\lim\limits_{x \rightarrow \infty} x e^{-x} = 0$ gilt, da
der lineare langsamer als der exponentielle Term wächst.
Berechnung über den Faltungssatz:
Unter Anwendung des Faltungssatzes und Verwendung des Ergebnisses aus Aufgabenteil 2 folgt:
$\D (\mathcal{F}g(x))(t) = \sqrt{2\pi}\hat{f}(x)\, \hat{f}(x) = \frac{1}{\sqrt{2\pi}} \frac{1}{(1+it)^2}$
Aufgabe 4
Sei
$f(x) =
\begin{cases}
\D 0, & x < 0 \\
\D e^{-x}, & x \ge 0 \\
\end{cases}$ und
$g(x) =
\begin{cases}
\D 1, & 0 \le x \le 1 \\
\D 0, & \text{sonst} \\
\end{cases}$
Bestimmen Sie $f \ast g$.
Bestimmen Sie die Fouriertransformierte von $f \ast g$ mit Hilfe des Faltungssatzes.
Tipp
- Die Faltung ist definiert durch: $\D (f \ast g)(x) := \int_{-\infty}^{\infty}\,f(x-t)\,g(t)\,dt.$
- Der Faltungssatz lautet: $\D (\mathcal{F}(f \ast g)(x))(t) = \sqrt{2\pi}(\mathcal{F} f(x))(t) (\mathcal{F} g(x))(t)$
Lösung
Aufgabenteil 1:
Die Faltung $(f \ast g)(x)$ lautet:
$(f \ast g)(x) =
\begin{cases}
\D 0, & x \le 0 \\
\D \frac{1}{\sqrt{2\pi}}\int_0^x e^{-t}\,dt =\frac{1}{\sqrt{2\pi}}(1-e^{-x}), &0 \le x \le 1 \\
\D \frac{1}{\sqrt{2\pi}}\int_{x-1}^x e^{-t}\,dt = \frac{1}{\sqrt{2\pi}}(e^{-(x-1)}-e^{-x}) = \frac{1}{\sqrt{2\pi}}e^{-x} (e-1), &1 \le x \le \infty \\
\end{cases}$
Aufgabenteil 2:
$\D \hat{f}(t) = \frac{1}{\sqrt{2\pi}}\int_0^{\infty} e^{-x} e^{-i t x}\,dx = \frac{1}{\sqrt{2\pi}}\int_0^{\infty} e^{(-1-it)x}\,dx = \frac{1}{\sqrt{2\pi}}\frac{1}{1+it} = \frac{1}{\sqrt{2\pi}}\frac{1-it}{1+t^2}$
$\D \hat{g}(t) = \frac{1}{\sqrt{2\pi}}\int_0^{1} e^{-i t x}\,dx = \frac{1}{\sqrt{2\pi}}\frac{1}{-i t} e^{-i t x} \Bigg|_0^1 = \frac{1}{\sqrt{2\pi}}\frac{i}{t} (e^{-i t} - 1)$
Mit dem Faltungssatz folgt:
$\D \widehat{(f \ast g)}(t) =\sqrt{2\pi} \hat{f}(t) \hat{g}(t) = \frac{1}{\sqrt{2\pi}}\frac{i(1-it)}{t(1+t^2)} (e^{-i t} -1)$