Aufgabe 1
Sei $E_1$ die Ebene $\D \vec{x}=\V{3\\0\\2}+\alpha\V{1\\-1\\0}+\beta \V{2\\2\\1}$ und $E_2 $ die Ebene durch $\D \V{1\\1\\1}$, $\D \V{0\\5\\1}$ und $\D \V{1\\0\\0}$ definiert.Bestimmen Sie den Winkel zwischen den Normalenvektoren von $E_1$ und $E_2$.
Tipp
Berechne einen Normalenvektor $\vec{n}_1$ von $E_1$ und zwei Richtungsvektoren von $E_2$ und damit einen Normalenvektor $\vec{n}_2$ von $E_2$.
Lösung
Mit $\vec{n}_1=\V{1\\-1\\0}\times\V{2\\2\\1}=\V{-1\\-1\\4}$ und
$\vec{n}_2=\V{1\\-4\\0}\times \V{0\\1\\1}=\V{ -4\\-1\\1}$
ist $\D\cos \angle (\vec{n}_1,\vec{n}_2)=\frac{\vec{n}_1\cdot\vec{n}_2}{|\vec{n}_1|\cdot|\vec{n}_2|}=\frac{9}{18}=\frac{1}{2}$.
Der Winkel beträgt $\D \frac{\pi}{3}$ oder $60 ^\circ$.
Zur Bestimmung von $\vec{n}_2$ wurde $\vec{v}_1 = \V{1 \\ 1 \\ 1}$ als Stützvektor gesetzt und die Richtungsvektoren $\vec{r}_1, \vec{r}_2$ über
$\vec{r}_1 = \vec{v}_1 - \vec{v}_2 = \V{1 \\ 1 \\ 1} - \V{0 \\ 5 \\ 1} = \V{1 \\ -4 \\ 0}$ bzw.
$\vec{r}_2 = \vec{v}_1 - \vec{v}_3 = \V{1 \\ 1 \\ 1} - \V{1 \\ 0 \\ 0} = \V{0 \\ 1 \\ 1}$ berechnet.
Die Ebengleichung in Parameterform für $E_2$ würde also $\vec{x} = \vec{v}_1 + \alpha \, \vec{r}_1 + \beta \, \vec{r}_2 = \V{1 \\ 1 \\ 1} + \alpha \V{1 \\ -4 \\ 0} + \beta \V{0 \\ 1 \\1}$ lauten.
ist $\D\cos \angle (\vec{n}_1,\vec{n}_2)=\frac{\vec{n}_1\cdot\vec{n}_2}{|\vec{n}_1|\cdot|\vec{n}_2|}=\frac{9}{18}=\frac{1}{2}$.
Der Winkel beträgt $\D \frac{\pi}{3}$ oder $60 ^\circ$.
Zur Bestimmung von $\vec{n}_2$ wurde $\vec{v}_1 = \V{1 \\ 1 \\ 1}$ als Stützvektor gesetzt und die Richtungsvektoren $\vec{r}_1, \vec{r}_2$ über
$\vec{r}_1 = \vec{v}_1 - \vec{v}_2 = \V{1 \\ 1 \\ 1} - \V{0 \\ 5 \\ 1} = \V{1 \\ -4 \\ 0}$ bzw.
$\vec{r}_2 = \vec{v}_1 - \vec{v}_3 = \V{1 \\ 1 \\ 1} - \V{1 \\ 0 \\ 0} = \V{0 \\ 1 \\ 1}$ berechnet.
Die Ebengleichung in Parameterform für $E_2$ würde also $\vec{x} = \vec{v}_1 + \alpha \, \vec{r}_1 + \beta \, \vec{r}_2 = \V{1 \\ 1 \\ 1} + \alpha \V{1 \\ -4 \\ 0} + \beta \V{0 \\ 1 \\1}$ lauten.
Aufgabe 2
Sei $f:\bbbr^2\to \bbbr^2$, $f(x,y)=(xy,x+y)$. Untersuchen Sie $f$ auf Injektivität und Surjektivität.Tipp
$f$ ist surjektiv, wenn sich die Gleichung $f(x,y)=(u,v)$ für jedes Paar $(u,v)\in \bbbr^2$ lösen lässt.
$f$ ist injektiv, wenn die Gleichung $f(x,y)=(u,v)$ für jedes Paar $(u,v)\in \bbbr^2$ höchstens eine Lösung hat.
$f$ ist injektiv, wenn die Gleichung $f(x,y)=(u,v)$ für jedes Paar $(u,v)\in \bbbr^2$ höchstens eine Lösung hat.
Lösung
$f$ ist nicht injektiv wegen $f(1,-1)=f(-1,1)$.
$f$ ist nicht surjektiv: aus $xy=u$, $x+y=u$ folgt
$y=u-x$, also $x(u-x)=v\LR x^2-ux+v=0$ $\D\LR x_{1,2}=-\frac{u}{2}\pm\frac{1}{4}\sqrt{u^2-4v}$.
Man sieht, dass diese Gleichung für $u^4<4v$ unlösbar ist.
Außerdem sieht man, dass die Lösung im Allgemeinen nicht eindeutig ist, also noch nicht einmal die Nicht-Injektivität.
$f$ ist nicht surjektiv: aus $xy=u$, $x+y=u$ folgt
$y=u-x$, also $x(u-x)=v\LR x^2-ux+v=0$ $\D\LR x_{1,2}=-\frac{u}{2}\pm\frac{1}{4}\sqrt{u^2-4v}$.
Man sieht, dass diese Gleichung für $u^4<4v$ unlösbar ist.
Außerdem sieht man, dass die Lösung im Allgemeinen nicht eindeutig ist, also noch nicht einmal die Nicht-Injektivität.
Aufgabe 3
Bestimmen Sie die Umkehrfunktion zu$\D \renewcommand{\arraystretch}{2} f(x)=\left\{ \begin{array}{ll}\D 4-\frac{1}{x-1}&~\text{ für }~ x<1\\ x+1 &~\text{ für }~ 1\le x\le 3\\ -x^2+6x-7 &~ \text{ für } 3 < x \end{array} \right.$
und skizzieren Sie den Graphen von $f$.
Tipp
Bestimmen Sie die Wertebereiche der einzelnen Teilfunktionen.
Das sind dann die Definitionsbereiche der Teile der Umkehrfunktion.
Zum Umkehren vertauschen Sie $x$ und $y$ und lösen Sie nach $y$ auf.
Das sind dann die Definitionsbereiche der Teile der Umkehrfunktion.
Zum Umkehren vertauschen Sie $x$ und $y$ und lösen Sie nach $y$ auf.
Lösung
Im Folgenden werden für jede drei Teilfunktionen $f_1(x), f_2(x)$ und $f_3(x)$ drei Umkehrfunktionen $f_1^{-1}(x), f_2^{-1}(x), f_3^{-1}(x)$ bestimmt.
$\fbox{ $\D f_1(x) = 4 - \frac{1}{x-1}$ für $x < 1$}$
Setze: $f_1(x) = y$
$\begin{array}{lccc} & \D y & = & \D 4 - \frac{1}{x-1} \\ \LR & \D y-4 & = & \D -\frac{1}{x-1} \\ \LR & \D \frac{1}{4-y} & = & \D x-1 \\ \LR & \D x & = & \D 1 + \frac{1}{4-y} \end{array}$
Vertausche $x$ mit $y$, um $f_1^{-1}(x)$ zu erhalten: $f_1^{-1}(x) = \D 1 + \frac{1}{4-x}$.
Für den Definitionsbereich von $f_1(x)$ gilt $x < 1$. Diese Forderung gilt dann wiederum für den Wertebereich von $f_1^{-1}(x)$.
Damit $f_1^{-1}(x) < 1$ gilt, muss $x > 4$ für die Umkehrfunktion gelten.
Also: $f_1^{-1}(x) = \D 1 + \frac{1}{4-x}$ für $x > 4$.
$\fbox{$\D f_2(x) = x + 1$ für $1 \le x \le 3$}$
$\begin{array}{lccc} & \D y & = & \D x+1 \\ \LR & \D x & = & \D y-1 \\ \end{array}$
Analog folgt: $f_2^{-1}(x) = x - 1$
Für den Definitionsbereich von $f_2(x)$ gilt $1 \le x \le 3$.
Damit $1 \le f_2^{-1}(x) \le 3$ gilt, folgt also für $x$ der Umkehrfunktion: $2 \le x \le 4$.
$\fbox{$\D f_3(x) = -x^2 + 6 x - 7$ für $x > 3$}$
$\begin{array}{lccc} & \D y & = & \D -x^2+6x-7 \\ \LR & \D x^2-6x+7+y & = & 0 \\ \LR & \D x & = & 3 \pm \sqrt{2-y} \\ \end{array}$
$\D f_3^{-1}(x) = 3 \pm \sqrt{2-x}$
Da für den Wertebereich $f_3^{-1}(x) > 3$ gilt, folgt für die Umkehrfunktion: $f_3^{-1} = 3 + \sqrt{2-x}$ für $x < 2$
Gesamtlösung:
$\D f^{-1}(x)=\left\{ \begin{array}{ll} 3+\sqrt{2-x}&~\text{ für }~ x<2\\ x-1 &~\text{ für }~ 2\le x\le 4\\ \D 1+\frac{1}{4-x} &~ \text{ für } x > 4 \end{array} \right.$
Graph von $f(x)$:
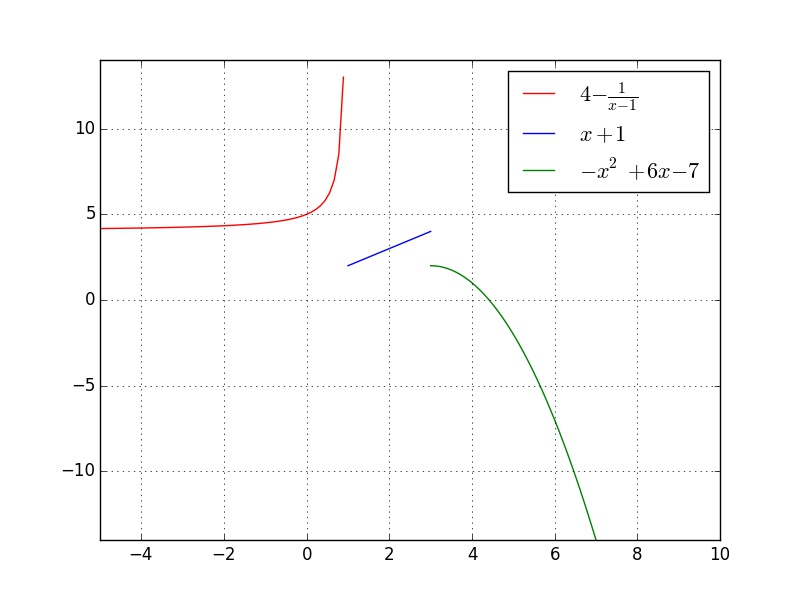
(Klicken zum Vergrößern)
$\fbox{ $\D f_1(x) = 4 - \frac{1}{x-1}$ für $x < 1$}$
Setze: $f_1(x) = y$
$\begin{array}{lccc} & \D y & = & \D 4 - \frac{1}{x-1} \\ \LR & \D y-4 & = & \D -\frac{1}{x-1} \\ \LR & \D \frac{1}{4-y} & = & \D x-1 \\ \LR & \D x & = & \D 1 + \frac{1}{4-y} \end{array}$
Vertausche $x$ mit $y$, um $f_1^{-1}(x)$ zu erhalten: $f_1^{-1}(x) = \D 1 + \frac{1}{4-x}$.
Für den Definitionsbereich von $f_1(x)$ gilt $x < 1$. Diese Forderung gilt dann wiederum für den Wertebereich von $f_1^{-1}(x)$.
Damit $f_1^{-1}(x) < 1$ gilt, muss $x > 4$ für die Umkehrfunktion gelten.
Also: $f_1^{-1}(x) = \D 1 + \frac{1}{4-x}$ für $x > 4$.
$\fbox{$\D f_2(x) = x + 1$ für $1 \le x \le 3$}$
$\begin{array}{lccc} & \D y & = & \D x+1 \\ \LR & \D x & = & \D y-1 \\ \end{array}$
Analog folgt: $f_2^{-1}(x) = x - 1$
Für den Definitionsbereich von $f_2(x)$ gilt $1 \le x \le 3$.
Damit $1 \le f_2^{-1}(x) \le 3$ gilt, folgt also für $x$ der Umkehrfunktion: $2 \le x \le 4$.
$\fbox{$\D f_3(x) = -x^2 + 6 x - 7$ für $x > 3$}$
$\begin{array}{lccc} & \D y & = & \D -x^2+6x-7 \\ \LR & \D x^2-6x+7+y & = & 0 \\ \LR & \D x & = & 3 \pm \sqrt{2-y} \\ \end{array}$
$\D f_3^{-1}(x) = 3 \pm \sqrt{2-x}$
Da für den Wertebereich $f_3^{-1}(x) > 3$ gilt, folgt für die Umkehrfunktion: $f_3^{-1} = 3 + \sqrt{2-x}$ für $x < 2$
Gesamtlösung:
$\D f^{-1}(x)=\left\{ \begin{array}{ll} 3+\sqrt{2-x}&~\text{ für }~ x<2\\ x-1 &~\text{ für }~ 2\le x\le 4\\ \D 1+\frac{1}{4-x} &~ \text{ für } x > 4 \end{array} \right.$
Graph von $f(x)$:

(Klicken zum Vergrößern)
Aufgabe 4
Bestimmen Sie die Lösungsmenge von $\D 2\frac{|x-2|}{x+1}>1$.Tipp
Unterscheiden Sie die Fälle $x<-1$, $-1< x<2$ und $x\ge 2$.
Lösung
Es ist direkt ersichtlich, dass $x = -1$ nicht zur Lösungsmenge gehört: $ \{-1\} \notin \bbbl$
Es werden drei Fälle unterschieden.
1. Fall: $x < -1, \qquad |x-2| = -(x-2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{-(x-2)}{x+1} &>& 1 &\Bigg| \cdot (x+1) \\ \LR &-2x+4 &<& x+1 &\Bigg| \text{Das Ungleichheitszeichen dreht sich um, da $(x+1) < 0$}\\ \\ \LR &-3x &<& -3 &\\ \\ \LR &x &>& 1 & \end{array}$
Dies widerspricht $x < -1$. Die Lösungsmenge $\bbbl_1$ ist leer.
2. Fall: $-1 < x < 2, \qquad |x-2| = -(x-2)$
Da $(x+1) > 0$ erhalten wir analog zum ersten Fall: $x < 1$.
Zusammen mit der Bedingung $-1 < x < 2$ ist die Lösungsmenge $\bbbl_2 = (-1, 1)$.
3. Fall: $x > 2, \qquad |x-2| = +(x-2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{x-2}{x+1} &>& 1 & \\ \\ \LR &2x-4 &>& x+1 &\\ \\ \LR &x &>& 5 &\\ \end{array}$
Hieraus folgt: $\bbbl_3 = (5, \infty)$.
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 \cup \bbbl_3 = (-1, 1) \cup (5, \infty)$
Es werden drei Fälle unterschieden.
1. Fall: $x < -1, \qquad |x-2| = -(x-2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{-(x-2)}{x+1} &>& 1 &\Bigg| \cdot (x+1) \\ \LR &-2x+4 &<& x+1 &\Bigg| \text{Das Ungleichheitszeichen dreht sich um, da $(x+1) < 0$}\\ \\ \LR &-3x &<& -3 &\\ \\ \LR &x &>& 1 & \end{array}$
Dies widerspricht $x < -1$. Die Lösungsmenge $\bbbl_1$ ist leer.
2. Fall: $-1 < x < 2, \qquad |x-2| = -(x-2)$
Da $(x+1) > 0$ erhalten wir analog zum ersten Fall: $x < 1$.
Zusammen mit der Bedingung $-1 < x < 2$ ist die Lösungsmenge $\bbbl_2 = (-1, 1)$.
3. Fall: $x > 2, \qquad |x-2| = +(x-2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{x-2}{x+1} &>& 1 & \\ \\ \LR &2x-4 &>& x+1 &\\ \\ \LR &x &>& 5 &\\ \end{array}$
Hieraus folgt: $\bbbl_3 = (5, \infty)$.
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 \cup \bbbl_3 = (-1, 1) \cup (5, \infty)$
Aufgabe 5
Bestimmen Sie die Lösungsmenge von $\D \frac{|x|}{4+x}+|x+2|>1$.Tipp
Unterscheiden Sie die Fälle $x < -4$, $-4< x < -2$, $-2\le x < 0$ und $x\ge 0$.
Lösung
Es werden vier Fälle unterschieden.
1. Fall: $x < -4, \qquad |x| = -(x), \qquad |x+2| = -(x+2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{-(x)}{4+x} -(x+2) &>& 1 & \\ \\ \LR &\D \frac{-x-(x+2)(4+x)}{4+x} &>& 1 &\Bigg| \cdot (x+4)\\ \\ \LR &-x-x^2-6x-8 &<& 4+x & \text{wegen $(x+4) < 0$ dreht sich das Ungleichheitszeichen um.}\\ \\ \LR &x^2+8x+12 &>& 0 & \\ \\ \LR &(x+6)(x+2) &>& 0 & \end{array}$
Zusammen mit der Bedingung $x < -4$ lautet die Lösungsmenge $\bbbl_1 = (-\infty, -6)$
2. Fall: $-4 < x < -2, \qquad |x| = -(x), \qquad |x+2| = -(x+2)$
Analog zum ersten Fall erhalten wir: $(x+6)(x+2) < 0$, da $(x+4) > 0$)
Mit der Bedingung $-4 < x < -2$ folgt für die Lösungsmenge $\bbbl_2 = (-4, -2)$.
3. Fall: $-2 < x < 0, \qquad |x| = -(x), \qquad |x+2| = +(x+2)$
$\begin{array}{lcccl} \quad &\D \frac{-(x)}{4+x} +(x+2) &>& 1 & \\ \\ \LR &\D \frac{-x+(x+2)(4+x)}{4+x} &>& 1 &\\ \\ \LR &-x+x^2+6x+8 &>& 4+x &\\ \\ \LR &x^2+4x+4 &>& 0 & \\ \\ \LR &(x+2)^2 &>& 0 & \end{array}$
Die Lösungsmenge lautet somit $\bbbl_3 = (-2, 0)$
4. Fall: $x \ge 0, \qquad |x| = +(x), \qquad |x+2| = +(x+2)$
$\begin{array}{lcccl} \quad &\D\frac{+(x)}{4+x} +(x+2) &>& 1 & \\ \\ \LR &\D \frac{x+(x+2)(4+x)}{4+x} &>& 1 &\\ \\ \LR &x^2+6x+8 &>& 4 &\\ \\ \LR &x^2+6x+4 &>& 0 & \\ \\ \LR &(x+3+\sqrt{5})(x+3-\sqrt{5})&>& 0 & \end{array}$
Mit der Bedingung $x \ge 0$ lautet die Lösungsmenge $\bbbl_4 = (0, \infty)$
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 \cup \bbbl_3 \cup \bbbl_4 = (-\infty, -6) \cup (-4, -2) \cup (-2, 0) \cup (0, \infty)$
1. Fall: $x < -4, \qquad |x| = -(x), \qquad |x+2| = -(x+2)$
$\begin{array}{lcccl} \quad &\D 2 \frac{-(x)}{4+x} -(x+2) &>& 1 & \\ \\ \LR &\D \frac{-x-(x+2)(4+x)}{4+x} &>& 1 &\Bigg| \cdot (x+4)\\ \\ \LR &-x-x^2-6x-8 &<& 4+x & \text{wegen $(x+4) < 0$ dreht sich das Ungleichheitszeichen um.}\\ \\ \LR &x^2+8x+12 &>& 0 & \\ \\ \LR &(x+6)(x+2) &>& 0 & \end{array}$
Zusammen mit der Bedingung $x < -4$ lautet die Lösungsmenge $\bbbl_1 = (-\infty, -6)$
2. Fall: $-4 < x < -2, \qquad |x| = -(x), \qquad |x+2| = -(x+2)$
Analog zum ersten Fall erhalten wir: $(x+6)(x+2) < 0$, da $(x+4) > 0$)
Mit der Bedingung $-4 < x < -2$ folgt für die Lösungsmenge $\bbbl_2 = (-4, -2)$.
3. Fall: $-2 < x < 0, \qquad |x| = -(x), \qquad |x+2| = +(x+2)$
$\begin{array}{lcccl} \quad &\D \frac{-(x)}{4+x} +(x+2) &>& 1 & \\ \\ \LR &\D \frac{-x+(x+2)(4+x)}{4+x} &>& 1 &\\ \\ \LR &-x+x^2+6x+8 &>& 4+x &\\ \\ \LR &x^2+4x+4 &>& 0 & \\ \\ \LR &(x+2)^2 &>& 0 & \end{array}$
Die Lösungsmenge lautet somit $\bbbl_3 = (-2, 0)$
4. Fall: $x \ge 0, \qquad |x| = +(x), \qquad |x+2| = +(x+2)$
$\begin{array}{lcccl} \quad &\D\frac{+(x)}{4+x} +(x+2) &>& 1 & \\ \\ \LR &\D \frac{x+(x+2)(4+x)}{4+x} &>& 1 &\\ \\ \LR &x^2+6x+8 &>& 4 &\\ \\ \LR &x^2+6x+4 &>& 0 & \\ \\ \LR &(x+3+\sqrt{5})(x+3-\sqrt{5})&>& 0 & \end{array}$
Mit der Bedingung $x \ge 0$ lautet die Lösungsmenge $\bbbl_4 = (0, \infty)$
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 \cup \bbbl_3 \cup \bbbl_4 = (-\infty, -6) \cup (-4, -2) \cup (-2, 0) \cup (0, \infty)$
Aufgabe 6
Bestimmen Sie die Lösungsmenge von $\D \frac{1}{x+1}-x\le -\frac{1}{2}$.Tipp
Unterscheiden Sie die Fälle $x< -1$ und $x>-1$.
<
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
<
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
Lösung
Es ist direkt ersichtlich, dass $x = -1$ nicht zur Lösungsmenge gehört: $\{-1\} \notin \bbbl$
Es werden deshalb zwei Fälle unterschieden.
1. Fall: $x < -1$
$\begin{array}{lccll} \quad &\D \frac{1}{x+1} -x &<& \D - \frac{1}{2} & \\ \\ \LR &\D \frac{1}{x+1} &<& \D x - \frac{1}{2} & \Bigg| \cdot (x+1)\\ \\ \LR &1 &>&\D x^2+x-\frac{1}{2}x - \frac{1}{2}& \text{das Ungleichheitszeichen dreht sich um, da$(x+1) < 0$}\\ \\ \LR &0 &>&\D x^2 + \frac{1}{2}x - \frac{3}{2} & \\ \\ \LR &0 &>&\D x^2 + \frac{1}{2} x + \left( \frac{1}{4})^2 \right) - \left( \frac{1}{4} \right)^2 - \frac{3}{2} & \\ \\ \LR &0 &>&\D \left( x+\frac{1}{4} \right)^2 - \frac{25}{16} \\ \\ \LR &\D \Big|x+\frac{1}{4} \Big| &<& \D \sqrt{\frac{25}{16}} = \frac{5}{4} & \\ \end{array}$
Somit gehören alle $x$ zur Lösungsmenge, deren Abstand $\D < \frac{5}{4}$ zum Punkt $\D x = - \frac{1}{4}$ ist. Also: $\D -\frac{6}{4} = - \frac{3}{2} < x < 1$
Dies kann sich am besten durch das Zeichen eines Zahlenstrahls verdeutlicht werden.
Mit $x < -1$ lautet die Lösungsmenge: $\bbbl_1 = (-\frac{3}{2}, -1)$
2. Fall: $x > -1$
Wir erhalten:
$\begin{array}{lccll} \LR &\D \Big|x+\frac{1}{4} \Big| &>& \D \sqrt{\frac{25}{16}} = \frac{5}{4} & \\ \end{array}$
Es gehören also alle $x$ zur Lösungsmenge, deren Abstand $\D > \frac{5}{4}$ zu $\D x = - \frac{1}{4}$ ist. Dies ist für alle $x$ mit $\D -\frac{3}{2} > x > 1$ erfüllt.
Mit der Bedingung $x > -1$ lautet die Lösungsmenge: $\bbbl_2 = (1, \infty)$
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 = (-\frac{3}{2}, -1) \cup (1, \infty)$
Es werden deshalb zwei Fälle unterschieden.
1. Fall: $x < -1$
$\begin{array}{lccll} \quad &\D \frac{1}{x+1} -x &<& \D - \frac{1}{2} & \\ \\ \LR &\D \frac{1}{x+1} &<& \D x - \frac{1}{2} & \Bigg| \cdot (x+1)\\ \\ \LR &1 &>&\D x^2+x-\frac{1}{2}x - \frac{1}{2}& \text{das Ungleichheitszeichen dreht sich um, da$(x+1) < 0$}\\ \\ \LR &0 &>&\D x^2 + \frac{1}{2}x - \frac{3}{2} & \\ \\ \LR &0 &>&\D x^2 + \frac{1}{2} x + \left( \frac{1}{4})^2 \right) - \left( \frac{1}{4} \right)^2 - \frac{3}{2} & \\ \\ \LR &0 &>&\D \left( x+\frac{1}{4} \right)^2 - \frac{25}{16} \\ \\ \LR &\D \Big|x+\frac{1}{4} \Big| &<& \D \sqrt{\frac{25}{16}} = \frac{5}{4} & \\ \end{array}$
Somit gehören alle $x$ zur Lösungsmenge, deren Abstand $\D < \frac{5}{4}$ zum Punkt $\D x = - \frac{1}{4}$ ist. Also: $\D -\frac{6}{4} = - \frac{3}{2} < x < 1$
Dies kann sich am besten durch das Zeichen eines Zahlenstrahls verdeutlicht werden.
Mit $x < -1$ lautet die Lösungsmenge: $\bbbl_1 = (-\frac{3}{2}, -1)$
2. Fall: $x > -1$
Wir erhalten:
$\begin{array}{lccll} \LR &\D \Big|x+\frac{1}{4} \Big| &>& \D \sqrt{\frac{25}{16}} = \frac{5}{4} & \\ \end{array}$
Es gehören also alle $x$ zur Lösungsmenge, deren Abstand $\D > \frac{5}{4}$ zu $\D x = - \frac{1}{4}$ ist. Dies ist für alle $x$ mit $\D -\frac{3}{2} > x > 1$ erfüllt.
Mit der Bedingung $x > -1$ lautet die Lösungsmenge: $\bbbl_2 = (1, \infty)$
Die Gesamtlösung lautet: $\bbbl = \bbbl_1 \cup \bbbl_2 = (-\frac{3}{2}, -1) \cup (1, \infty)$
Aufgabe 7
Für welche $x\in \bbbr$ ist $x|x|\le 3x-2 $?Tipp
Unterscheiden Sie die Fälle $x<0$ und $x\ge 0$.
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
Lösung
1. Fall: $x < 0, \qquad |x| = -(x)$
$\begin{array}{lrcll} \quad &\D -x^2 &\le& 3x-2 & \\ \\ \LR &\D 0 &\le& \D x^2+3x-2 = x^2+3x+ \left( \frac{3}{2} \right)^2 - \left( \frac{3}{2} \right)^2 - 2 &\\ \\ \LR &0 &\le& \D \left( x+\frac{3}{2} \right)^2 - \frac{17}{4} &\\ \\ \LR &\D \left( x+\frac{3}{2} \right)^2 &\ge&\D \frac{17}{4}& \\ \\ \LR &\D \Big|x+\frac{3}{2} \Big| &\ge&\D \sqrt{\frac{17}{4}} = \frac{\sqrt{17}}{2} & \\ \end{array}$
Durch das Aufzeichnen eines Zahlenstrahls kann man sich verdeutlichen, wie die Lösungsmenge lauten muss.
Alle $x$, deren Abstand zu $\D x = -\frac{3}{2}$ größer-gleich $\D \frac{\sqrt{17}}{2}$ beträgt, gehören zur Lösungsmenge.
Zusammen mit $x < 0$ lautet diese: $\D \bbbl_1 = \left( -\infty, -\frac{\sqrt{17}-3}{2} \right]$
2. Fall: $x \ge 0, \qquad |x| = +(x)$
$\begin{array}{lrcll} \quad &\D x^2 &\le& 3x-2 & \\ \\ \LR &\D x^2-3x+2 &\le& 0 &\\ \\ \LR &\D x^2-3x + \left( \frac{3}{2} \right)^2 - \left( \frac{3}{2} \right)^2 + 2 &\le& 0 &\\ \\ \LR &\D \left( x-\frac{3}{2} \right)^2 - \frac{1}{4} &\le&\D 0& \\ \\ \LR &\D \Big|x-\frac{3}{2} \Big| &\le&\D \sqrt{\frac{1}{4}} = \frac{1}{2} & \\ \end{array}$
Diese Ungleichung wird von allen $x$ mit $1 \le x \le 2$ erfüllt.
Zusammen mit $x \ge 0$ folgt: $\bbbl_2 = [1, 2]$.
Die Gesamtlösung lautet also: $\D \bbbl = \bbbl_1 \cup \bbbl_2 = \left( -\infty, -\frac{\sqrt{17}-3}{2} \right] \cup [1, 2]$
Aufgabe 8
Bestimmen Sie Menge aller $x\in \bbbr$ mit $\D \frac{1}{|x-2|}-|x+2|<-2$.Tipp
Multiplizieren Sie zunächst mit dem Nenner.
Unterscheiden Sie die Fälle $x<-2$, $-2\le x<2$ und $x\ge 2$.
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
Unterscheiden Sie die Fälle $x<-2$, $-2\le x<2$ und $x\ge 2$.
Lösen Sie dann die Ungleichung mit quadratischer Ergänzung.
Lösung
Es ist direkt ersichtlich, dass $x = 2$ nicht zur Lösungsmenge gehört: $\{ 2 \} \notin \bbbl$
Multiplizieren mit dem Nenner (Vereinfachung):
$\begin{array}{lrcll} \quad &\D \frac{1}{|x-2|} -|x+2| &<& -2 & \\ \\ \LR &\D 1 - |x+2| |x-2| &<& -2 |x-2| &\\ \end{array}$
1. Fall: $x < -2, \qquad |x+2| = -(x+2), \qquad |x-2| = -(x-2)$
$\begin{array}{lrcll} \quad &\D 1 - (x+2)(x-2) &<& 2(x-2) = 2x-4 &\\ \\ \LR &\D 1 - x^2+4-2x+4 &<& 0 &\\ \\ \LR &\D x^2+2x+1-1-9 &>& 0 &\\ \\ \LR &(x+1)^2 &>& 10 & \\ \\ \LR &|x+1| &>& \sqrt{10} & \end{array}$
Anstatt die Lösungsmenge über den Abstandsbegriff zu ermitteln (s. Aufgabe 7 und 8), kann nun auch eine weitere Fallunterscheidung
vorgenommen werden.
Fall 1.1: $x+1 < 0 \LR x < -1, \qquad |x+1| = -(x+1)$
$\begin{array}{lrcll} \quad &\D -(x+1) &>& \sqrt{10} &\\ \\ \LR &\D x+1 &<& -\sqrt{10} &\\ \\ \LR &\D x &<& -\sqrt{10} -1 &\\ \end{array}$
Fall 1.2: $x+1 > 0 \LR x > -1, \qquad |x+1| = +(x+1)$
$\begin{array}{lrcll} \quad &\D x+1 &>& \sqrt{10} &\\ \\ \LR &\D x &>& \sqrt{10} - 1 &\\ \end{array}$
Zusammen mit der Bedingung $x < -2$ lautet die Lösungsmenge: $\bbbl_1 = (-\infty, - \sqrt{10} -1)$
2. Fall: $-2 < x < 2, \qquad |x+2| = +(x+2), \qquad |x-2| = -(x-2)$
$\begin{array}{lrcll} \quad &\D 1 + (x+2)(x-2) &<& 2x-4 &\\ \\ \LR &\D 1 + x^2-4-2x+4 &<& 0 &\\ \\ \LR &\D x^2-2x+1 &>& 0 &\\ \\ \LR &(x-1)^2 &<& 0 & \\ \\ \LR &|x-1| &<& 0 & \end{array}$
Es gibt keine Lösung für diese Ungleichung.
3. Fall $x \ge 2, \qquad |x+2| = +(x+2), \qquad |x-2| = +(x-2)$
$\begin{array}{lrcll} \quad &\D 1 - x^2+4+2x-4 &<& 0 &\\ \\ \LR &\D x^2-2x-1 &>& 0 &\\ \\ \LR &\D x^2-2x+1-1-1 &>& 0 &\\ \\ \LR &(x-1)^2 -2 &<& 0 & \\ \\ \LR &|x-1| &<& \sqrt{2} & \end{array}$
Die Lösungsmenge lautet: $\bbbl_3 = (1+ \sqrt{2}, +\infty)$
Somit folgt für die Gesamtlösung: $\bbbl_1 \cup \bbbl_2 \cup \bbbl_3 = (-\infty, -\sqrt{10}-1) \cup (1+ \sqrt{2}, +\infty)$
Multiplizieren mit dem Nenner (Vereinfachung):
$\begin{array}{lrcll} \quad &\D \frac{1}{|x-2|} -|x+2| &<& -2 & \\ \\ \LR &\D 1 - |x+2| |x-2| &<& -2 |x-2| &\\ \end{array}$
1. Fall: $x < -2, \qquad |x+2| = -(x+2), \qquad |x-2| = -(x-2)$
$\begin{array}{lrcll} \quad &\D 1 - (x+2)(x-2) &<& 2(x-2) = 2x-4 &\\ \\ \LR &\D 1 - x^2+4-2x+4 &<& 0 &\\ \\ \LR &\D x^2+2x+1-1-9 &>& 0 &\\ \\ \LR &(x+1)^2 &>& 10 & \\ \\ \LR &|x+1| &>& \sqrt{10} & \end{array}$
Anstatt die Lösungsmenge über den Abstandsbegriff zu ermitteln (s. Aufgabe 7 und 8), kann nun auch eine weitere Fallunterscheidung
vorgenommen werden.
Fall 1.1: $x+1 < 0 \LR x < -1, \qquad |x+1| = -(x+1)$
$\begin{array}{lrcll} \quad &\D -(x+1) &>& \sqrt{10} &\\ \\ \LR &\D x+1 &<& -\sqrt{10} &\\ \\ \LR &\D x &<& -\sqrt{10} -1 &\\ \end{array}$
Fall 1.2: $x+1 > 0 \LR x > -1, \qquad |x+1| = +(x+1)$
$\begin{array}{lrcll} \quad &\D x+1 &>& \sqrt{10} &\\ \\ \LR &\D x &>& \sqrt{10} - 1 &\\ \end{array}$
Zusammen mit der Bedingung $x < -2$ lautet die Lösungsmenge: $\bbbl_1 = (-\infty, - \sqrt{10} -1)$
2. Fall: $-2 < x < 2, \qquad |x+2| = +(x+2), \qquad |x-2| = -(x-2)$
$\begin{array}{lrcll} \quad &\D 1 + (x+2)(x-2) &<& 2x-4 &\\ \\ \LR &\D 1 + x^2-4-2x+4 &<& 0 &\\ \\ \LR &\D x^2-2x+1 &>& 0 &\\ \\ \LR &(x-1)^2 &<& 0 & \\ \\ \LR &|x-1| &<& 0 & \end{array}$
Es gibt keine Lösung für diese Ungleichung.
3. Fall $x \ge 2, \qquad |x+2| = +(x+2), \qquad |x-2| = +(x-2)$
$\begin{array}{lrcll} \quad &\D 1 - x^2+4+2x-4 &<& 0 &\\ \\ \LR &\D x^2-2x-1 &>& 0 &\\ \\ \LR &\D x^2-2x+1-1-1 &>& 0 &\\ \\ \LR &(x-1)^2 -2 &<& 0 & \\ \\ \LR &|x-1| &<& \sqrt{2} & \end{array}$
Die Lösungsmenge lautet: $\bbbl_3 = (1+ \sqrt{2}, +\infty)$
Somit folgt für die Gesamtlösung: $\bbbl_1 \cup \bbbl_2 \cup \bbbl_3 = (-\infty, -\sqrt{10}-1) \cup (1+ \sqrt{2}, +\infty)$
Aufgabe 9
Für welche $x\in \bbbr$ ist $2|x-3|+|x+3|<18-2x$ ?Tipp
Unterscheiden Sie die Fälle $x<-3$, $-3\le x<3$ und $x\ge 3$ und lösen Sie die Beträge jeweils auf.
Lösung
Für $x<-3$ sind die Inhalte beider Beträge negativ, also hat man
$-2(x-3)-(x+3)<18-2x$
$\Leftrightarrow -3x+3<18-2x$
$\Leftrightarrow x>-15$
Damit ist $\bbbl_1=(-15,-3)$ ein Teil der Lösungsmenge.
Für $-3\le x<3$ ist nur $x-3$ negativ. Man hat also
$2(x-3)-(x+3)<18-2x$
$\LR x-9<18-2x$
$\LR 3x<27$
$\LR x<9$
Damit ist der ganze Teilbereich $\bbbl_2=[-3,3)$ Teil der Lösungsmenge
Für $x\ge 3$ sind die Inhalte beider Beträge positiv.
$2(x-3)+(x+3)<18-2x$
$\LR 3x-3<18-2x$
$\LR 5x<21$
$\LR x<\dfrac{21}{5}$
Damit ist das Intervall $\bbbl_3=[3,\dfrac{21}{5})$ Teil der Lösungsmenmge
Die Gesamtlösungsmenge ist $\bbbl=\bbbl_1\cup\bbbl_2\cup\bbbl_3=(-15,\dfrac{21}{5})$