Aufgabe 1
$M$ sei der Teil des Zylindermantels $M=\{(x,y,z)\in \bbbr^3\mid\,x^2+y^2=4, 0\le z\le 2, y\ge 0 \}$. $M$ sei dabei so orientiert, dass der Normalenvektor eine nichtnegative $y$-Komponente hat, $C$ sei die Randkurve von $M$.$\vec{w}$ sei das Vektorfeld $\vec{w}=(x^2z, -2yz-\frac{z^2}{2},0)$.
Berechnen Sie $\D \int_C \vec{w}\,d\vec{x}$ sowohl direkt als auch mit einem geeigneten Integralsatz.
Tipp
- Zerlege $C$ in vier Teilkurven und wähle geeignete Parametrisierungen.
- Nicht alle Kurvenintegral müssen explizit berechnet werden!
- Der Satz von Stokes lautet: $\D \int_O \, \vec{w}\, d\vec{x} = \int_M \, \mathrm{rot} \, \vec{w}\,d \vec{o}$
Lösung
1. direkte Berechnung:
Es müssen vier Kurven parametrisiert werden (s. Skizze).
$\begin{align} C_1: \quad &\vec{\phi_1}(t) = \V{2 \\ 0 \\ t}, \qquad &\dot{\vec{\phi_1}}(t) = \V{0 \\ 0 \\ 1} \qquad &,t \in [0, 2) \\ C_2: \quad &\vec{\phi_2}(t) = \V{2 \cos t \\ 2 \sin t \\ 0}, \qquad &\dot{\vec{\phi_2}}(t) = \V{-2 \sin t \\ 2 \cos t \\ 0} \qquad &,t \in [0, \pi) \\ -C_3: \quad &\vec{\phi_3}(t) = \V{2 \cos t \\ 2 \sin t \\ 2}, \qquad &\dot{\vec{\phi_3}}(t) = \V{-2 \sin t \\ 2 \cos t \\ 0} \qquad &,t \in [0, \pi) \\ C_4: \quad &\vec{\phi_4}(t) = \V{-2 \\ 0 \\ t}, \qquad &\dot{\vec{\phi_4}}(t) = \V{0 \\ 0 \\ 1} \qquad &,t \in [0, 2) \end{align}$
Da $\D \vec{w}(x,y,z=0) = 0$ ist, ist auch $\D \int_{C_2}\,\vec{w}\,d\vec{x} = 0$.
Wegen $\dot{\vec{\phi_1}}(t) = \dot{\vec{\phi_4}}(t) = \V{0 \\ 0 \\ 1}$ auf $C_1$ und $C_2$, ist $\D \int_{C_1}\,\vec{w}\,d \vec{x} = \int_{C_4}\,\vec{w}\,d \vec{x} = 0$.
Für das orientierte Kurvenintegral entlang $-C_3$ gilt:
$\begin{align} \D - \int_{-C_3}\,\vec{w}\,d \vec{x} &= - \D \int_{t=0}^{\pi}\,\vec{w}({\vec{\phi_3}}(t)) \cdot \dot{\vec{\phi_3}}\,dt \\ \\ &= \D - \int_{t=0}^{\pi} \V{8 \cos^2 t \\ -8 \sin t - 2 \\ 0}\, \V{-2 \sin t \\ 2 \cos t \\ 0}\, dt \\ \\ &= 16 \int_{t=0}^{\pi}\,(\cos^2 t \sin t + \sin t \cos t + \frac{\cos t}{4})\, dt \\ \\ &= 16 \Big[ - \frac{\cos^3 t}{3} + \frac{\sin^2 t}{2} + \frac{\sin t}{4} \Big]_0^{\pi} \\ \\ &= 16 \Big[ -(-\frac{1}{3}) + \frac{1}{3} \Big] = \frac{32}{3} \end{align}$
Somit ist lautet das Ergebnis $\D \int_{C}\, \vec{w}\,d\vec{x} = \frac{32}{3}$.
2. Berechnung mithilfe des Satz von Stokes
Der Satz von Stokes lauet: $\D \int_O \, \vec{w}\, d\vec{x} = \int_M \, \mathrm{rot} \, \vec{w}\,d \vec{o}$
Die Rotation des Vektorfeldes $\vec{w}$ berechnet sich wie folgt:
$\D \mathrm{rot} \, \vec{w} = \V{\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z}} \times \V{x^2 z \\ -2yz - \frac{z^2}{2}\\0} = \V{2y+z \\ x^2 \\ 0}$.
Eine geeignete Parametrisierung der Mantelfläche $M$ lautet:
$\D M: \quad \vec{\phi}(t,z) = \V{2 \cos t \\ 2 \sin t \\ z}, \qquad 0 < z < 2 $ und $ 0 < t < \pi$
Für den Normalenvektor gilt: $\vec{\phi}_t \times \vec{\phi}_z = \V{-2 \sin t \\ 2 \cos t \\ 0} \times \V{0 \\ 0 \\ 1} = \V{2 \cos t \\ 2 \sin t \\ 0}$.
Nach Aufgabenstellung ist $M$ so orientiert, dass der Normalenvektor eine nichtnegative $y$-Komponente hat. Der berechnete Normalenvektor
erfüllt dies und muss somit nicht geändert werden.
Berechnung des Flächenintegrals:
$\begin{align} \D \int_M \, \vec{w}\,d \vec{o} &= \int_{t=0}^{\pi} \int_{z=0}^2 \, \vec{w}(\vec{\phi}(t)) \, (\vec{\phi}_t \times \vec{\phi}_z)\, dzdt \\ \\ &= \int_{t=0}^{\pi} \int_{z=0}^2 \, \V{4 \sin t + z \\ 4 \cos^2 t \\ 0} \V{2 \cos t \\ 2 \sin t \\ 0} \, dzdt \\ \\ &= \int_{t=0}^{\pi} \int_{z=0}^2 \, (8 \sin t \cos t + 2 z \cos t + 8 \cos^2 t \sin t)\, dzdt \\ \\ &= \int_{t=0}^{\pi} (16 \sin t \cos t + 4 \cos t + 16 \cos^2 t \sin t) \, dt \\ \\ &= (8 \sin^2 t + 4 \sin t - \frac{16}{3} \cos^3t) \Bigg|_0^{\pi} = \frac{32}{3} \end{align}$
Es müssen vier Kurven parametrisiert werden (s. Skizze).
$\begin{align} C_1: \quad &\vec{\phi_1}(t) = \V{2 \\ 0 \\ t}, \qquad &\dot{\vec{\phi_1}}(t) = \V{0 \\ 0 \\ 1} \qquad &,t \in [0, 2) \\ C_2: \quad &\vec{\phi_2}(t) = \V{2 \cos t \\ 2 \sin t \\ 0}, \qquad &\dot{\vec{\phi_2}}(t) = \V{-2 \sin t \\ 2 \cos t \\ 0} \qquad &,t \in [0, \pi) \\ -C_3: \quad &\vec{\phi_3}(t) = \V{2 \cos t \\ 2 \sin t \\ 2}, \qquad &\dot{\vec{\phi_3}}(t) = \V{-2 \sin t \\ 2 \cos t \\ 0} \qquad &,t \in [0, \pi) \\ C_4: \quad &\vec{\phi_4}(t) = \V{-2 \\ 0 \\ t}, \qquad &\dot{\vec{\phi_4}}(t) = \V{0 \\ 0 \\ 1} \qquad &,t \in [0, 2) \end{align}$
Da $\D \vec{w}(x,y,z=0) = 0$ ist, ist auch $\D \int_{C_2}\,\vec{w}\,d\vec{x} = 0$.
Wegen $\dot{\vec{\phi_1}}(t) = \dot{\vec{\phi_4}}(t) = \V{0 \\ 0 \\ 1}$ auf $C_1$ und $C_2$, ist $\D \int_{C_1}\,\vec{w}\,d \vec{x} = \int_{C_4}\,\vec{w}\,d \vec{x} = 0$.
Für das orientierte Kurvenintegral entlang $-C_3$ gilt:
$\begin{align} \D - \int_{-C_3}\,\vec{w}\,d \vec{x} &= - \D \int_{t=0}^{\pi}\,\vec{w}({\vec{\phi_3}}(t)) \cdot \dot{\vec{\phi_3}}\,dt \\ \\ &= \D - \int_{t=0}^{\pi} \V{8 \cos^2 t \\ -8 \sin t - 2 \\ 0}\, \V{-2 \sin t \\ 2 \cos t \\ 0}\, dt \\ \\ &= 16 \int_{t=0}^{\pi}\,(\cos^2 t \sin t + \sin t \cos t + \frac{\cos t}{4})\, dt \\ \\ &= 16 \Big[ - \frac{\cos^3 t}{3} + \frac{\sin^2 t}{2} + \frac{\sin t}{4} \Big]_0^{\pi} \\ \\ &= 16 \Big[ -(-\frac{1}{3}) + \frac{1}{3} \Big] = \frac{32}{3} \end{align}$
Somit ist lautet das Ergebnis $\D \int_{C}\, \vec{w}\,d\vec{x} = \frac{32}{3}$.
2. Berechnung mithilfe des Satz von Stokes
Der Satz von Stokes lauet: $\D \int_O \, \vec{w}\, d\vec{x} = \int_M \, \mathrm{rot} \, \vec{w}\,d \vec{o}$
Die Rotation des Vektorfeldes $\vec{w}$ berechnet sich wie folgt:
$\D \mathrm{rot} \, \vec{w} = \V{\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z}} \times \V{x^2 z \\ -2yz - \frac{z^2}{2}\\0} = \V{2y+z \\ x^2 \\ 0}$.
Eine geeignete Parametrisierung der Mantelfläche $M$ lautet:
$\D M: \quad \vec{\phi}(t,z) = \V{2 \cos t \\ 2 \sin t \\ z}, \qquad 0 < z < 2 $ und $ 0 < t < \pi$
Für den Normalenvektor gilt: $\vec{\phi}_t \times \vec{\phi}_z = \V{-2 \sin t \\ 2 \cos t \\ 0} \times \V{0 \\ 0 \\ 1} = \V{2 \cos t \\ 2 \sin t \\ 0}$.
Nach Aufgabenstellung ist $M$ so orientiert, dass der Normalenvektor eine nichtnegative $y$-Komponente hat. Der berechnete Normalenvektor
erfüllt dies und muss somit nicht geändert werden.
Berechnung des Flächenintegrals:
$\begin{align} \D \int_M \, \vec{w}\,d \vec{o} &= \int_{t=0}^{\pi} \int_{z=0}^2 \, \vec{w}(\vec{\phi}(t)) \, (\vec{\phi}_t \times \vec{\phi}_z)\, dzdt \\ \\ &= \int_{t=0}^{\pi} \int_{z=0}^2 \, \V{4 \sin t + z \\ 4 \cos^2 t \\ 0} \V{2 \cos t \\ 2 \sin t \\ 0} \, dzdt \\ \\ &= \int_{t=0}^{\pi} \int_{z=0}^2 \, (8 \sin t \cos t + 2 z \cos t + 8 \cos^2 t \sin t)\, dzdt \\ \\ &= \int_{t=0}^{\pi} (16 \sin t \cos t + 4 \cos t + 16 \cos^2 t \sin t) \, dt \\ \\ &= (8 \sin^2 t + 4 \sin t - \frac{16}{3} \cos^3t) \Bigg|_0^{\pi} = \frac{32}{3} \end{align}$
Aufgabe 2
Sei $H=\{ (x,y)\,|\, x^2+y^2\le 4,\, 0\le y \}$ und $\vec{v}$ das Vektorfeld $\D\vec{v}(x,y)=\V{2xy \\ x^2+y^2}$.Berechnen Sie $\D \int_H \text{div}\,\,\vec{v}\,d(x,y) $ sowohl direkt wie auch mit einem geeigneten Integralsatz.
Tipp
- Es handelt sich bei $H$ um einen Halbkreis mit dem Radius $r = 2$.
- Zerlege die Randkurve $C$ von $H$ in zwei Teilkurven.
Lösung
1. direkte Berechnung:
Um das Integral $\D \int_C \, \vec{v} \cdot \vec{n}\,ds$ zu bestimmen, muss die Kurve $C$ in zwei
Kurven zerlegt werden.
$\D \int_C \, \vec{v} \cdot \vec{n}\,ds = \int_{C_1} \, \vec{v} \cdot \vec{n}\,ds + \int_{C_2} \, \vec{v} \cdot \vec{n}\,ds$
Die Kurve wird über $\vec{\phi}_1(t) = \V{2 \cos t \\ 2 \sin t} \quad ,0 < t < \pi$ parametrisiert. Mit $|\vec{\phi}_{1_t}| = 2$ berechnet
sich das Kurvenintegral wie folgt:
$\begin{align} \D \int_{C_1} \, \vec{v} \cdot \vec{n}\,ds &= \int_{C_1}\, \V{2xy \\ x^2 + y^2} \cdot \underbrace{\frac{1}{2} \V{x \\ y}}_{\vec{n}}\, ds \\ \\ &= \int_0^{\pi} \, \V{8 \sin t \cos t \\ 4} \, \V{\cos t \\ \sin t} 2\, dt \\ \\ &= 8 \int_0^{\pi} \, \Big[\sin t \cos^2 t + \sin t \Big]\,dt \\ \\ &= \D 8 \Big[- \frac{2 \cos^3 t}{3} - \cos t \Big]_0^{\pi} = \frac{80}{3} \end{align}$
Die Parametrisierung für die Kurve $C_2$ lautet: $\vec{\phi}_2(t) = \V{t \\ 0}, \;-2 < t < 2$ mit dem Normalenvektor $\vec{n} = \V{0 \\ -1}$.
$\begin{align} \D \int_{C_2} \, \vec{v} \cdot \vec{n}\,ds &= \int_{t=-2}^{2} \, \V{0 \\ t^2} \, \V{0 \\ -1}\, dt \\ \\ &= \int_{t=-2}^{2} \, -t^2\, dt \\ \\ &= - \frac{t^3}{3} \Bigg|_{-2}^{2} = - \frac{16}{3} \end{align}$
Somit ist $\D \int_C \, \vec{v} \cdot \vec{n}\,ds = \frac{64}{3}$.
2. Berechnung mithilfe des Satz von Gauß im $\bbbr^2$:
Es gilt: $\D \iint_H \, \mathrm{div} \, \vec{v}\, dxdy = \int_C \, \vec{v} \cdot \vec{n} \, ds$.
Mit $\mathrm{div}\,\vec{v} = 4y$ und der Einführung von Polarkoordinaten
$\V{x \\ y} := \V{r \cos \rho \\ r \sin \rho} \quad ,0 < r < 2 \quad ,0 < \rho < \pi \quad ,d(x,y) = r\,d(r, \rho)$
berechnet sich das Integral wie folgt:
$\begin{align} \D \iint_H \, \mathrm{div} \, \vec{v}\, d(x,y) &= \int_{r=0}^{2} \int_{\rho=0}^{\pi} \, 4 r \sin \rho \,r\,d\rho dr \\ \\ &= 4 \int_{r=0}^{2} \, r^2\,dr \, \int_{\rho=0}^{\pi} \, \sin \rho \, d \rho \\ \\ &= 4 \cdot \frac{8}{3} = \frac{64}{3} \end{align}$
Um das Integral $\D \int_C \, \vec{v} \cdot \vec{n}\,ds$ zu bestimmen, muss die Kurve $C$ in zwei
Kurven zerlegt werden.
$\D \int_C \, \vec{v} \cdot \vec{n}\,ds = \int_{C_1} \, \vec{v} \cdot \vec{n}\,ds + \int_{C_2} \, \vec{v} \cdot \vec{n}\,ds$
Die Kurve wird über $\vec{\phi}_1(t) = \V{2 \cos t \\ 2 \sin t} \quad ,0 < t < \pi$ parametrisiert. Mit $|\vec{\phi}_{1_t}| = 2$ berechnet
sich das Kurvenintegral wie folgt:
$\begin{align} \D \int_{C_1} \, \vec{v} \cdot \vec{n}\,ds &= \int_{C_1}\, \V{2xy \\ x^2 + y^2} \cdot \underbrace{\frac{1}{2} \V{x \\ y}}_{\vec{n}}\, ds \\ \\ &= \int_0^{\pi} \, \V{8 \sin t \cos t \\ 4} \, \V{\cos t \\ \sin t} 2\, dt \\ \\ &= 8 \int_0^{\pi} \, \Big[\sin t \cos^2 t + \sin t \Big]\,dt \\ \\ &= \D 8 \Big[- \frac{2 \cos^3 t}{3} - \cos t \Big]_0^{\pi} = \frac{80}{3} \end{align}$
Die Parametrisierung für die Kurve $C_2$ lautet: $\vec{\phi}_2(t) = \V{t \\ 0}, \;-2 < t < 2$ mit dem Normalenvektor $\vec{n} = \V{0 \\ -1}$.
$\begin{align} \D \int_{C_2} \, \vec{v} \cdot \vec{n}\,ds &= \int_{t=-2}^{2} \, \V{0 \\ t^2} \, \V{0 \\ -1}\, dt \\ \\ &= \int_{t=-2}^{2} \, -t^2\, dt \\ \\ &= - \frac{t^3}{3} \Bigg|_{-2}^{2} = - \frac{16}{3} \end{align}$
Somit ist $\D \int_C \, \vec{v} \cdot \vec{n}\,ds = \frac{64}{3}$.
2. Berechnung mithilfe des Satz von Gauß im $\bbbr^2$:
Es gilt: $\D \iint_H \, \mathrm{div} \, \vec{v}\, dxdy = \int_C \, \vec{v} \cdot \vec{n} \, ds$.
Mit $\mathrm{div}\,\vec{v} = 4y$ und der Einführung von Polarkoordinaten
$\V{x \\ y} := \V{r \cos \rho \\ r \sin \rho} \quad ,0 < r < 2 \quad ,0 < \rho < \pi \quad ,d(x,y) = r\,d(r, \rho)$
berechnet sich das Integral wie folgt:
$\begin{align} \D \iint_H \, \mathrm{div} \, \vec{v}\, d(x,y) &= \int_{r=0}^{2} \int_{\rho=0}^{\pi} \, 4 r \sin \rho \,r\,d\rho dr \\ \\ &= 4 \int_{r=0}^{2} \, r^2\,dr \, \int_{\rho=0}^{\pi} \, \sin \rho \, d \rho \\ \\ &= 4 \cdot \frac{8}{3} = \frac{64}{3} \end{align}$
Aufgabe 3
Sei $K$ der durch $\V{x\\y\\z}=\V{r \cos t\\r\sin t\\z}$ mit $0\le t\le 2\pi$, $0\le z\le 1$ und $0\le r \le 2-z$ definierte Kegelstumpf.Der Normalenvektor zeige aus $K$ heraus.
- Berechnen Sie die Gesamtoberfläche von $K$.
- Berechnen Sie den Fluß des Vektorfeldes $\vec{v}=(P,Q,R)=(y,-x,2z)$ durch die Oberfläche von $K$ mit einem geeigneten Integralsatz.
- Berechnen Sie den Fluß von $\vec{v}$ durch den Kegelmantel, d.h. den Teil der Oberfläche, der durch $0\le t\le 2\pi$, $0\le z\le 1$ und $r = 2-z$ beschrieben ist.
Tipp
- Aufgabenteil 1 und 3: Der Radius $r$ der Kegelmantels ist $z$-abhängig $r = 2 - z$.
- Aufgabenteil 2: Der Satz von Gauß lautet: $\D \iint_O \vec{v}\,d\vec{F} = \iiint_K \mathrm{div}\,\vec{v}\,d(x,y,z)$
Lösung
Aufgabenteil 1:
Bei Boden und Deckel des Kegelstumpfes handelt es sich um Kreise in $x$-$y$-Ebene mit den Radien $r_B = 2$ und $r_D = 1$.
Mit der bekannten Formel für eine Kreisfläche $O_{\text{Kreis}} = \pi\,r^2$ folgt also
$O_B = \pi\,r_B^2 = 4\pi, \qquad O_D = \pi\,r_D^2 = \pi$.
Der Kegelstumpfmantel $M$ wird als Rotationsfläche mit Radius $r(z) = 2-z$ berechnet.
Die Parametrisierung lautet also
$\vec{\phi}(t, z) = \V{(2-z) \cos t \\ (2-z) \sin t \\ z}$ mit $(\vec{\phi}_t \times \ \vec{\phi}_z) = \V{-(2-z) \sin t \\ (2-z) \cos t \\ 0} \times \V{- \cos t \\ - \sin t \\ 1} = (2-z) \V{\cos t \\ \sin t \\ 1}$
und $||\vec{\phi}_t \times \ \vec{\phi}_z|| = \sqrt{(2-z)^2(\cos^2 t + \sin^2 t + 1)} = \sqrt{2(2-z)^2}= \sqrt{2}\, (2-z).$
Das (skalare) Oberflächenintegral lautet somit:
$\begin{align} O_M &= \int_{z=0}^{1} \int_{t=0}^{2 \pi} ||\vec{\phi}_t \times \ \vec{\phi}_z||\,dtdz \\ \\ &= \int_{z=0}^{1} \int_{t=0}^{2 \pi} \sqrt{2}\, 2-z\,dtdz \\ \\ &= \sqrt{2}\,2\pi (2z-\frac{z^2}{2}) \Bigg|_0^1 \\ \\ &= \sqrt{2}\,2\pi (2-\frac{1}{2}) = 3\,\sqrt{2}\pi \end{align}$
Aufgabenteil 2:
Wir verwenden den Satz von Gauß: $\D \iint_O \vec{v}\,d\vec{F} = \iiint_K \mathrm{div}\,\vec{v}\,d(x,y,z)$
Mit $\mathrm{div}\,\vec{v} = 2$ folgt also:
$\begin{align} \D \iint_O \vec{v}\,d\vec{F} &= 2 \cdot \mathrm{vol}_3 (K) = 2 \int_{z=0}^1 \int_{r=0}^{2-z} \int_{\rho = 0}^{2 \pi} r\,d\rho dr dz \\ \\ &= 2 \pi \int_{z=0}^1 r^2 \Bigg|_0^{2-z}\,dz \\ \\ &= 2 \pi \int_{z=0}^1 (2-z)^2\,dz = 2 \pi (-\frac{1}{3}) (2-z)^3 \Bigg|_0^1 \\ \\ &= - \frac{2\pi}{3} (1-8) = \frac{14}{3} \pi \end{align}$
Aufgabenteil 3:
Für das Flussintegral gilt:
$\D \iint_M \vec{v}\,d\vec{F} = \iint_{M'} \vec{v}(\vec{\phi}(t, z))\,(\vec{\phi}_t \times \ \vec{\phi}_z)\,dtdz$
Mit den Ergebnissen aus Aufgabenteil 1 folgt:
$\begin{align} \D \iint_M \vec{v}\,d\vec{F} &= \int_{t=0}^{2\pi} \int_{z=0}^{1} (2-z) \V{(2-z) \sin t \\ -(2-z) \cos t \\ 2z} \, \V{\cos t \\ \sin t \\ 1}\,dzdt \\ \\ &= \int_{t=0}^{2\pi} \int_{z=0}^{1} (4z-2z^2)\,dzdt \\ \\ &= 2\pi (2z^2- \frac{2}{3} z^3) \Bigg|_0^1 = \frac{8}{3}\pi \end{align}$
Bei Boden und Deckel des Kegelstumpfes handelt es sich um Kreise in $x$-$y$-Ebene mit den Radien $r_B = 2$ und $r_D = 1$.
Mit der bekannten Formel für eine Kreisfläche $O_{\text{Kreis}} = \pi\,r^2$ folgt also
$O_B = \pi\,r_B^2 = 4\pi, \qquad O_D = \pi\,r_D^2 = \pi$.
Der Kegelstumpfmantel $M$ wird als Rotationsfläche mit Radius $r(z) = 2-z$ berechnet.
Die Parametrisierung lautet also
$\vec{\phi}(t, z) = \V{(2-z) \cos t \\ (2-z) \sin t \\ z}$ mit $(\vec{\phi}_t \times \ \vec{\phi}_z) = \V{-(2-z) \sin t \\ (2-z) \cos t \\ 0} \times \V{- \cos t \\ - \sin t \\ 1} = (2-z) \V{\cos t \\ \sin t \\ 1}$
und $||\vec{\phi}_t \times \ \vec{\phi}_z|| = \sqrt{(2-z)^2(\cos^2 t + \sin^2 t + 1)} = \sqrt{2(2-z)^2}= \sqrt{2}\, (2-z).$
Das (skalare) Oberflächenintegral lautet somit:
$\begin{align} O_M &= \int_{z=0}^{1} \int_{t=0}^{2 \pi} ||\vec{\phi}_t \times \ \vec{\phi}_z||\,dtdz \\ \\ &= \int_{z=0}^{1} \int_{t=0}^{2 \pi} \sqrt{2}\, 2-z\,dtdz \\ \\ &= \sqrt{2}\,2\pi (2z-\frac{z^2}{2}) \Bigg|_0^1 \\ \\ &= \sqrt{2}\,2\pi (2-\frac{1}{2}) = 3\,\sqrt{2}\pi \end{align}$
Aufgabenteil 2:
Wir verwenden den Satz von Gauß: $\D \iint_O \vec{v}\,d\vec{F} = \iiint_K \mathrm{div}\,\vec{v}\,d(x,y,z)$
Mit $\mathrm{div}\,\vec{v} = 2$ folgt also:
$\begin{align} \D \iint_O \vec{v}\,d\vec{F} &= 2 \cdot \mathrm{vol}_3 (K) = 2 \int_{z=0}^1 \int_{r=0}^{2-z} \int_{\rho = 0}^{2 \pi} r\,d\rho dr dz \\ \\ &= 2 \pi \int_{z=0}^1 r^2 \Bigg|_0^{2-z}\,dz \\ \\ &= 2 \pi \int_{z=0}^1 (2-z)^2\,dz = 2 \pi (-\frac{1}{3}) (2-z)^3 \Bigg|_0^1 \\ \\ &= - \frac{2\pi}{3} (1-8) = \frac{14}{3} \pi \end{align}$
Aufgabenteil 3:
Für das Flussintegral gilt:
$\D \iint_M \vec{v}\,d\vec{F} = \iint_{M'} \vec{v}(\vec{\phi}(t, z))\,(\vec{\phi}_t \times \ \vec{\phi}_z)\,dtdz$
Mit den Ergebnissen aus Aufgabenteil 1 folgt:
$\begin{align} \D \iint_M \vec{v}\,d\vec{F} &= \int_{t=0}^{2\pi} \int_{z=0}^{1} (2-z) \V{(2-z) \sin t \\ -(2-z) \cos t \\ 2z} \, \V{\cos t \\ \sin t \\ 1}\,dzdt \\ \\ &= \int_{t=0}^{2\pi} \int_{z=0}^{1} (4z-2z^2)\,dzdt \\ \\ &= 2\pi (2z^2- \frac{2}{3} z^3) \Bigg|_0^1 = \frac{8}{3}\pi \end{align}$
Aufgabe 4
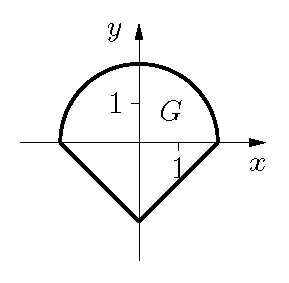
Sei $G$ das Gebiet in $\bbbr^2$ eingeschlossen von den Kurvenbögen$C_1: x^2+y^2=4, \; y\ge 0$, $C_2: x+y=-2, \;x\in[-2,0]$ und\
$C_3: x-y=2, \; x\in[0,2]$.
Berechnen Sie den Flächeninhalt von $G$ mit Hilfe des Satzes von Gauß .
Tipp
- Der Satz von Gauß im $\bbbr^2$ (auch Satz von Green genannt) lautet: $\D \iint_G \left( \frac{\partial g}{\partial x} (x,y) - \frac{\partial f}{\partial y}(x,y) \right) \,dxdy = \oint_C (f(x,y)\,dx + g(x,y)\,dy)$
- Wähle $f(x,y) = 0$ und $g(x,y) = 0$, um den Flächeninhalt zu berechnen.
- Wähle geeignete Parametrisierungen für die Teilkruven $C_1$ bis $C_3$.
Lösung
Der Satz von Gauß im $\bbbr^2$ (auch Satz von Green genannt) lautet allgemein:
$\D \iint_G \left( \frac{\partial g}{\partial x} (x,y) - \frac{\partial f}{\partial y}(x,y) \right) \,dxdy = \oint_C (f(x,y)\,dx + g(x,y)\,dy)$
Um den Flächeninhalt von $G$ zu berechnen, wählen wir $f(x,y) = 0$ und $g(x,y) = x$.
Somit folgt: $\D \oint_C (f(x,y)\,dx + g(x,y)\,dy) = \oint_C x\,dy$
Es werden drei Teilkurven $C_1, C_2$ und $C_3$ parametrisiert.
$\begin{align} \D C_1: \V{x \\ y} &= \V{2 \cos t \\ 2 \sin t}, \quad 0 \le t \le \pi \\ \\ \int_{C_1} x\,dy &= \int_0^{\pi} 2 \cos t \cdot 2 \cos t\, dt = 4 \int_0^{\pi} \cos^2t\,dt = 4 \frac{\pi}{2} = 2\pi \end{align}$
$\begin{align} \D C_2: \V{x \\ y} &= \V{-2+t \\ -t}, \quad 0 \le t \le 2 \\ \\ \int_{C_2} x\,dy &= \int_0^{2} (-2+t)(-1), dt = \int_0^{2} (2-t)\,dt = \Big[2t - \frac{t^2}{2} \Big]_0^2 = 2 \end{align}$
$\begin{align} \D C_3: \V{x \\ y} &= \V{t \\ -2+t}, \quad 0 \le t \le 2 \\ \\ \int_{C_3} x\,dy &= \int_0^{2} t \cdot 1, dt = \int_0^{2} (2-t)\,dt = \frac{t^2}{2} \Bigg|_0^2 = 2 \end{align}$
Das Ergebnis lautet somit:
$\begin{align} \D \oint_C x\,dy &= \int_{C_1} x\,dy + \int_{C_2} x\,dy + \int_{C_2} x\,dy \\ \\ &= 2\pi + 4 \end{align}$
$\D \iint_G \left( \frac{\partial g}{\partial x} (x,y) - \frac{\partial f}{\partial y}(x,y) \right) \,dxdy = \oint_C (f(x,y)\,dx + g(x,y)\,dy)$
Um den Flächeninhalt von $G$ zu berechnen, wählen wir $f(x,y) = 0$ und $g(x,y) = x$.
Somit folgt: $\D \oint_C (f(x,y)\,dx + g(x,y)\,dy) = \oint_C x\,dy$
Es werden drei Teilkurven $C_1, C_2$ und $C_3$ parametrisiert.
$\begin{align} \D C_1: \V{x \\ y} &= \V{2 \cos t \\ 2 \sin t}, \quad 0 \le t \le \pi \\ \\ \int_{C_1} x\,dy &= \int_0^{\pi} 2 \cos t \cdot 2 \cos t\, dt = 4 \int_0^{\pi} \cos^2t\,dt = 4 \frac{\pi}{2} = 2\pi \end{align}$
$\begin{align} \D C_2: \V{x \\ y} &= \V{-2+t \\ -t}, \quad 0 \le t \le 2 \\ \\ \int_{C_2} x\,dy &= \int_0^{2} (-2+t)(-1), dt = \int_0^{2} (2-t)\,dt = \Big[2t - \frac{t^2}{2} \Big]_0^2 = 2 \end{align}$
$\begin{align} \D C_3: \V{x \\ y} &= \V{t \\ -2+t}, \quad 0 \le t \le 2 \\ \\ \int_{C_3} x\,dy &= \int_0^{2} t \cdot 1, dt = \int_0^{2} (2-t)\,dt = \frac{t^2}{2} \Bigg|_0^2 = 2 \end{align}$
Das Ergebnis lautet somit:
$\begin{align} \D \oint_C x\,dy &= \int_{C_1} x\,dy + \int_{C_2} x\,dy + \int_{C_2} x\,dy \\ \\ &= 2\pi + 4 \end{align}$
Aufgabe 5
Sei $\vec{v}(x,y,z)=\V{xz^2\\z\\1+y}$ und $Z$ der durch $x^2+y^2\le 4$, $0\le z\le1$ beschriebene Zylinder.Berechnen Sie den Fluß von $\vec{v}$ durch die Oberfläche von $Z$ sowohl direkt als auch mit Hilfe des Gaußschen Satzes.
Tipp
- Wähle Zylinderkoordinanten, um Deckel, Mantel und Boden des Zylinders zu parametrisieren.
- Der Satz von Gauß im $\bbbr^3$ lautet allgemein: $\D \iint_F\,\vec{v}(\vec{r})\,d\vec{o} = \iiint_G \mathrm{div}\,\vec{v}\,d(x,y,z)$
Lösung
1. direkte Berechnung
Um den Fluss durch die Zylinderoberfläche direkt zu berechen, muss der Zylinder in drei Teile zerlegt werden: Boden, Mantel, Deckel.
1.1 Boden des Zylinders ($z=0$):
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{r \cos \rho \\ r \sin \rho \\ 0}, \qquad \vec{\phi}_r \times \vec{\phi}_{\rho} = \V{\cos \rho \\ \sin \rho \\ 0} \times \V{-r \sin \rho \\ r \cos \rho \\ 0} = \V{0 \\ 0 \\ r}$
Der Normalenvektor zeigt in die falsche Richtung und wird mit einem Minuszeichen korrigiert: $\vec{\phi}_r \times \vec{\phi}_{\rho} = \V{0 \\ 0 \\ -r}$
Der Fluss durch den Boden berechnet sich wie folgt:
$\Phi_B = \D \int_{r=0}^2 \int_{\rho=0}^{2 \pi} \V{0 \\ 0 \\ 1 + r \sin \rho} \V{0 \\ 0 \\ -r}\, d\rho dr = - \int_{r=0}^2 2\pi r\, dr = -4 \pi$
1.2 Deckel des Zylinders ($z=1$):
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{r \cos \rho \\ r \sin \rho \\ 1}, \qquad \vec{\phi}_r \times \vec{\phi}_{\rho} = \V{\cos \rho \\ \sin \rho \\ 0} \times \V{-r \sin \rho \\ r \cos \rho \\ 0} = \V{0 \\ 0 \\ r}$
Der Normalenvektor zeigt in die richtige Richtung und muss nicht geändert werden.
$\Phi_D = \D \int_{r=0}^2 \int_{\rho=0}^{2 \pi} \V{r \cos \rho \\ 1 \\ 1 + r \sin \rho} \V{0 \\ 0 \\ r}\, d\rho dr = \int_{r=0}^2 2\pi r\, dr = 4 \pi$
1.3 Mantel des Zylinders:
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{2 \cos \rho \\ 2 \sin \rho \\ z}, \qquad \vec{\phi}_{\rho} \times \vec{\phi}_{z} = \V{- 2 \sin \rho \\ 2 \cos \rho \\ 0} \times \V{0 \\ 0 \\ 1} = \V{2 \cos \rho \\ 2 \sin \rho \\ 0}$
Der Normalenvektor zeigt in die richtige Richtung und muss nicht geändert werden.
$\D \Phi_M = \int_{z=0}^1 \int_{\rho=0}^{2 \pi} \V{2 \cos \rho z^2 \\ z \\ 1 + 2 \sin \rho} \V{2 \cos \rho \\ 2 \sin \rho \\ 0}\, d\rho dz = \int_{z=0}^1 4 \pi z^2\,dz = \frac{4}{3} \pi z^3 \Bigg|_0^1 = \frac{4}{3} \pi$
Der Gesamtfluss beträgt somit: $\D \Phi_G = -4 \pi + 4\pi + \frac{4}{3} \pi$
2. Berechnung mit Hilfe des Gaußschen Satzes:
Der Satz von Gauß im $\bbbr^3$ lautet allgemein: $\D \iint_F\,\vec{v}(\vec{r})\,d\vec{o} = \iiint_G \mathrm{div}\,\vec{v}\,d(x,y,z)$
Mit $\D \mathrm{div}\,\vec{v} = \frac{\partial}{\partial x} \, xz^2 + \frac{\partial}{\partial y}\, z + \frac{\partial}{\partial z}\,(1+y) = z^2$ folgt für den Fluss $\Phi$:
$\D \Phi_G = \int_{z=0}^1 \int_{r=0}^2 \int_{\rho=0}^{2 \pi} z^2 r \, d\rho dr dz = \frac{z^3}{3} \Bigg|_0^1 \, \frac{r^2}{2} \Bigg|_0^2 \, 2\pi =\frac{1}{3} \, 2\, 2\pi = \frac{4}{3} \pi$
Um den Fluss durch die Zylinderoberfläche direkt zu berechen, muss der Zylinder in drei Teile zerlegt werden: Boden, Mantel, Deckel.
1.1 Boden des Zylinders ($z=0$):
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{r \cos \rho \\ r \sin \rho \\ 0}, \qquad \vec{\phi}_r \times \vec{\phi}_{\rho} = \V{\cos \rho \\ \sin \rho \\ 0} \times \V{-r \sin \rho \\ r \cos \rho \\ 0} = \V{0 \\ 0 \\ r}$
Der Normalenvektor zeigt in die falsche Richtung und wird mit einem Minuszeichen korrigiert: $\vec{\phi}_r \times \vec{\phi}_{\rho} = \V{0 \\ 0 \\ -r}$
Der Fluss durch den Boden berechnet sich wie folgt:
$\Phi_B = \D \int_{r=0}^2 \int_{\rho=0}^{2 \pi} \V{0 \\ 0 \\ 1 + r \sin \rho} \V{0 \\ 0 \\ -r}\, d\rho dr = - \int_{r=0}^2 2\pi r\, dr = -4 \pi$
1.2 Deckel des Zylinders ($z=1$):
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{r \cos \rho \\ r \sin \rho \\ 1}, \qquad \vec{\phi}_r \times \vec{\phi}_{\rho} = \V{\cos \rho \\ \sin \rho \\ 0} \times \V{-r \sin \rho \\ r \cos \rho \\ 0} = \V{0 \\ 0 \\ r}$
Der Normalenvektor zeigt in die richtige Richtung und muss nicht geändert werden.
$\Phi_D = \D \int_{r=0}^2 \int_{\rho=0}^{2 \pi} \V{r \cos \rho \\ 1 \\ 1 + r \sin \rho} \V{0 \\ 0 \\ r}\, d\rho dr = \int_{r=0}^2 2\pi r\, dr = 4 \pi$
1.3 Mantel des Zylinders:
$\D \vec{\phi}(r, \rho) = \V{x \\ y \\ z} = \V{2 \cos \rho \\ 2 \sin \rho \\ z}, \qquad \vec{\phi}_{\rho} \times \vec{\phi}_{z} = \V{- 2 \sin \rho \\ 2 \cos \rho \\ 0} \times \V{0 \\ 0 \\ 1} = \V{2 \cos \rho \\ 2 \sin \rho \\ 0}$
Der Normalenvektor zeigt in die richtige Richtung und muss nicht geändert werden.
$\D \Phi_M = \int_{z=0}^1 \int_{\rho=0}^{2 \pi} \V{2 \cos \rho z^2 \\ z \\ 1 + 2 \sin \rho} \V{2 \cos \rho \\ 2 \sin \rho \\ 0}\, d\rho dz = \int_{z=0}^1 4 \pi z^2\,dz = \frac{4}{3} \pi z^3 \Bigg|_0^1 = \frac{4}{3} \pi$
Der Gesamtfluss beträgt somit: $\D \Phi_G = -4 \pi + 4\pi + \frac{4}{3} \pi$
2. Berechnung mit Hilfe des Gaußschen Satzes:
Der Satz von Gauß im $\bbbr^3$ lautet allgemein: $\D \iint_F\,\vec{v}(\vec{r})\,d\vec{o} = \iiint_G \mathrm{div}\,\vec{v}\,d(x,y,z)$
Mit $\D \mathrm{div}\,\vec{v} = \frac{\partial}{\partial x} \, xz^2 + \frac{\partial}{\partial y}\, z + \frac{\partial}{\partial z}\,(1+y) = z^2$ folgt für den Fluss $\Phi$:
$\D \Phi_G = \int_{z=0}^1 \int_{r=0}^2 \int_{\rho=0}^{2 \pi} z^2 r \, d\rho dr dz = \frac{z^3}{3} \Bigg|_0^1 \, \frac{r^2}{2} \Bigg|_0^2 \, 2\pi =\frac{1}{3} \, 2\, 2\pi = \frac{4}{3} \pi$
Aufgabe 6
Sei $\vec{v}=\V{y-x^2\\-xy\\0}$ und $D=\{(x,y,z)\in\bbbr^3, x^2+y^2\le 1, z=0 \}$ so orientiert, dass der Flächennormalenvektor eine positive $z$-Komponente hat.Berechnen Sie $\D \int_D \text{rot}\,\, \vec{v}\cdot \vec{N}\,d\sigma$ sowohl direkt wie auch mit dem Integralsatz von Stokes.
Tipp
- Die Menge $D$ beschreibt eine Kreisscheibe in $x$-$y$-Ebene mit dem Radius $r=1$ bei $z=0$.
- Der Satz von Stokes lautet allgemein: $\D \int_F \mathrm{rot}\,\vec{v}\,d\vec{o} = \int_C \vec{v}\,d\vec{r}$
Lösung
Der Satz von Stokes lautet allgemein: $\D \int_F \mathrm{rot}\,\vec{v}\,d\vec{o} = \int_C \vec{v}\,d\vec{r}$
1. Berechnung des Flächenintegrals:
Parametrisierung der Fläche $D$: $\D \vec{\phi}_D = \V{x \\ y \\ z} = \V{r \cos t \\ r \sin t \\ 0}, \quad 0 \le r \le 1, \quad 0 \le t \le 2 \pi$
Mit dem Flächennormalenvektor: $\vec{\phi}_r \times \vec{\phi}_t = \V{\cos t \\ \sin t \\ 0} \times \V{-r \sin t \\ r \cos t \\ 0} = \V{0 \\ 0 \\ r}$.
Die $z$-Komponente des Vektors positiv und muss somit nicht korrigiert werden.
Die Rotation des Vektorfeldes berechnet sich wie folgt: $\D \mathrm{rot}\,\vec{v} = \V{\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z}} \times \V{y-x^2 \\ -xy \\ 0} = \V{0 \\ 0 \\ -y-1}$
Berechnung des Flächenintegrals:
$\begin{align} \D \int_D \mathrm{rot}\,\vec{v}\,d\vec{o} &= \int_0^{2 \pi} \int_0^1 \mathrm{rot}\,\vec{v}(\vec{\phi}_D)\,(\vec{\phi}_r \times \vec{\phi}_t)\,drdt \\ \\ &= \int_0^{2 \pi} \int_0^1 \V{0 \\ 0 \\ -1-r \sin t} \V{0 \\ 0 \\ 1}\,drdt \\ \\ &= \int_0^{2 \pi} \left( -\frac{1}{2} - \frac{1}{3} \sin t \right)\,dt = - \pi \end{align}$
2. Berechnung des Kurvenintegrals:
Parametrisierung der Fläche $C$: $\vec{\phi}_C = \V{x \\ y \\ z} = \V{\cos t \\ \sin t \\ 0}, \quad 0 \le t \le 2 \pi$
Mit $\dot{\vec{\phi}} = \V{-\sin t \\ \cos t \\ 0}$ folgt:
$\begin{align} \D \int_C \vec{v}\,d\vec{r} &= \int_0^{2 \pi} \vec{v}(\vec{\phi}_C)\,\dot{\vec{\phi}}\,dt \\ \\ &= \int_0^{2 \pi} \V{\sin t - \cos^2 t \\ - \sin t \cos t \\ 0} \V{- \sin t \\ \cos t \\ 0}\,dt \\ \\ &= \int_0^{2 \pi} -\sin^2 t dt = -\pi \end{align}$
1. Berechnung des Flächenintegrals:
Parametrisierung der Fläche $D$: $\D \vec{\phi}_D = \V{x \\ y \\ z} = \V{r \cos t \\ r \sin t \\ 0}, \quad 0 \le r \le 1, \quad 0 \le t \le 2 \pi$
Mit dem Flächennormalenvektor: $\vec{\phi}_r \times \vec{\phi}_t = \V{\cos t \\ \sin t \\ 0} \times \V{-r \sin t \\ r \cos t \\ 0} = \V{0 \\ 0 \\ r}$.
Die $z$-Komponente des Vektors positiv und muss somit nicht korrigiert werden.
Die Rotation des Vektorfeldes berechnet sich wie folgt: $\D \mathrm{rot}\,\vec{v} = \V{\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z}} \times \V{y-x^2 \\ -xy \\ 0} = \V{0 \\ 0 \\ -y-1}$
Berechnung des Flächenintegrals:
$\begin{align} \D \int_D \mathrm{rot}\,\vec{v}\,d\vec{o} &= \int_0^{2 \pi} \int_0^1 \mathrm{rot}\,\vec{v}(\vec{\phi}_D)\,(\vec{\phi}_r \times \vec{\phi}_t)\,drdt \\ \\ &= \int_0^{2 \pi} \int_0^1 \V{0 \\ 0 \\ -1-r \sin t} \V{0 \\ 0 \\ 1}\,drdt \\ \\ &= \int_0^{2 \pi} \left( -\frac{1}{2} - \frac{1}{3} \sin t \right)\,dt = - \pi \end{align}$
2. Berechnung des Kurvenintegrals:
Parametrisierung der Fläche $C$: $\vec{\phi}_C = \V{x \\ y \\ z} = \V{\cos t \\ \sin t \\ 0}, \quad 0 \le t \le 2 \pi$
Mit $\dot{\vec{\phi}} = \V{-\sin t \\ \cos t \\ 0}$ folgt:
$\begin{align} \D \int_C \vec{v}\,d\vec{r} &= \int_0^{2 \pi} \vec{v}(\vec{\phi}_C)\,\dot{\vec{\phi}}\,dt \\ \\ &= \int_0^{2 \pi} \V{\sin t - \cos^2 t \\ - \sin t \cos t \\ 0} \V{- \sin t \\ \cos t \\ 0}\,dt \\ \\ &= \int_0^{2 \pi} -\sin^2 t dt = -\pi \end{align}$