Aufgabe 1
Sei $\gamma(t)=\V{\frac{2}{3}t^3+t\\t^2\\\sqrt{3}\,t}$, $0\le t\le 3$ und
$\vec{v}(x,y,z)=(y^2,2xy+z,y-1)^T$.
- Berechnen Sie die Länge der Kurve $\gamma$.
- Berechnen Sie $\int_\gamma \vec{v}\, d\vec{x}$ mit Hilfe eines
Potentials.
Tipp
Für die Bogenlänge einer Kurve gilt: $\ell_C = \int_{a}^{b} |\dot{\vec{\gamma}}(t)|\,dt$
Lösung
Berechnung der Kurvenlänge
Es ist $\D \dot\gamma(t)=\V{2t^2+1\\2t\\\sqrt{3}}$ und
$\begin{align}
\D ||\dot\gamma(t)||^2
&=4t^4+4t^2+1+4t^2+3 \\
&=4t^4+8t^2+4 \\
&=4(t^4+2t^2+1) \\
\end{align}$
und somit folgt
$\D ||\dot\gamma(t)||=2(t^2+1) $.
Die Kurvenlänge (s. Tipp) $L$ lautet:
$\D L=\int_0^3 2(t^2+1)\, dt= 2\Big(\frac{t^3}{2}+t\Big) \Bigg|_0^3= 2(9+3)=24$
Bestimmung eines Potentials $F$
Wir betrachten die $x$-Komponente des Vektorfeldes und nennen sie $F_x$.
Integration nach $x$ liefert einen Ausdruck für das Potential:
$F(x,y,z) = \int F_x\,dx = xy^2 + c_1(y,z)$
Um die Konstante $c_1(y,z)$ zu bestimmen, wird $F(x,y,z)$ partiell nach $y$ abgeleitet und mit der $y$-Komponente $F_y$ des Vektorfeldes verglichen.
$\begin{array}{crclc}
& &\D \frac{\partial}{\partial y} F(x,y,z) &= & F_y &\\
&\LR & \D 2xy+\frac{\partial}{\partial y}c_1(y,z) &= & 2xy + z & \Bigg| -2xy \text{ und Integration nach $y$} \\
&\LR & \D c_1(y,z) &= &yz + c_2(z) &
\end{array}$
Damit ist $ F(x,y,z)=x^2y+yz+c_2(z)$.
Analog erhalten wir durch Ableiten von $F(x,y,z)$ nach $z$ und
Vergleichen des Audrucks mit der $z$-Komponente $F_z$ eine Lösung für $c_2(z)$.
Aus $F_z = y-1$ folgt $\D \frac{\partial}{\partial z}c_2(z)=-1, \quad$ also $c_2(z)=-z+c_3$.
Alle Potentiale von $\vec{v}$ sind also $F(x,y,z)=xy^2+yz-z+c_3$, $c_3\in \bbbr$.
Damit beträgt der Wert des Kurvenintegrals (mit $c_3=0$):
$\begin{align}
\int_\gamma \vec{v}\, d\vec{x}
&= F(\gamma(3))-F(\gamma(0))= F(21,9,3\sqrt{3})-F(0,0,0)\\
&= 21\cdot 81+27\sqrt{3}-3\sqrt{3} \\
&= 1701+24\sqrt{3}
\end{align}$
Aufgabe 2
Sei $F(x,y)=(3x^2+2xy^2,2x^2y-2)$ und $W$ der durch die Strecke von $(0,2)$ nach $(2,0)$ gegebene Weg.
Berechnen Sie $\D \int_W F\cdot dX$ sowohl direkt als auch mit Hilfe eines Potentials.
Tipp
- Allgemeines Verfahren zur Berechnung eines Kurvenintegrals: $\D \int_a^b f(\phi(t))\phi'(t)\,dt$. Wobei $\D \phi(t)$ eine Parametrisierung des Weges von $a$ nach $b$ ist.
- Skizziere den Weg und wähle eine geeignete Parametrisierung.
Lösung
Definiere Weg $W$
$\D W:\,X(t) = \V{0 \\ 2} + t \V{2 \\ -2} =\V{2t \\ 2-2t}$ und damit $\D \dot{X}(t) = \V{2 \\ -2}, \quad 0 \le t \le 1$
Direkte Berechnung
$\begin{align}
\D \int_{W} F\,dX
&= \int_{0}^{1} \V{12t^2+4t(2-2t)^2 \\ 2\cdot4t^2(2-2t)-2}\,\V{2 \\ -2} dt \\
&= \D \int_{0}^{1} 2 (12t^2+4t(4-8t+4t^2))-2\cdot2\cdot4t^2(2-2t)+4\,dt \\
&= \D \int_{0}^{1} 2 (16t^3-20t^2+16t)-32t^2+32t^3+4\,dt \\
&= \D \int_{0}^{1} 32t^3-40t^2+32t-32t^2+32t^3+4\,dt \\
&= \D \int_{0}^{1} 64t^3-72t^2+32t+4\,dt \\
&= \D \left[ 16t^4-24t^2+16t^2+4t \right]_0^1 = 12
\end{align}$
Berechnung mithilfe eines Potentials $f(x,y)$
$F(x,y)=\V{f_x \\ f_y} = \V{3x^2+2xy^2 \\ 2x^2y-2}$
Integration von $f_x$ nach $x$, um einen Ausdruck für das Potential $f(x,y)$ zu bekommen:
$f(x,y) = \D \int f_x\,dx = x^3 +x^2y^2+C(y))$
Ableiten von $f(x,y)$ nach $y$ und Vergleich mit $f_y$:
$2x^2y+C'(y) \overset{!}{=} 2x^2y-2 \LR C'(y) = -2 \LR C(y) = -2y + C$
Somit lautet das Potential:
$\D f(x,y)=x^3+x^2 y^2-2y+C$.
Damit ist $\D \int_W F\,dX = \left[ (x^3+x^2y^2-2y)] \right]_{(0,2)}^{(2,0)} = 8+4 = 12$.
Aufgabe 3
Bestimmen Sie die Länge des durch $\gamma(t)=\V{\operatorname{arsinh}(t)\\\sqrt{1+t^2}\\\cosh(t)}$, $0\le t\le 1$ gegebenen Wegs.
Tipp
$\D \frac{d }{dx}\operatorname{arsinh} x=\frac{1}{\sqrt{1+x^2}}$
Lösung
Für die Länge $\ell_C$ einer Kurve gilt: $\D \ell_C := \int_0^1 |\dot{\gamma}(t)|\,dt$
Bestimmung von $\D |\dot{\gamma}(t)|$
$\D \dot{\gamma}(t) = \V{\frac{1}{\sqrt{1+t^2}} \\ \frac{t}{\sqrt{1+t^2}} \\ \sinh t}$ und damit $\D |\dot{\gamma}(t)|^2 = \frac{1}{1+t^2} + \frac{t^2}{1+t^2} + \sinh^2 t = \cosh^2 t$
Also ist $\D |\dot{\gamma}(t)| = \cosh t$
Somit beträgt die Länge der Kurve: $\D \ell_C = \int_0^1 |\dot{\gamma}(t)| = \int_0^1 \cosh t = \left[ \sinh \right]_0^1 = \sinh 1 \approx 1.175$
Aufgabe 4
Die Kurve $y=x^3$, $0\le x\le 1$ rotiert im $\bbbr^3$ um die $x$-Achse.
- Berechnen Sie den Inhalt der dabei entstehenden Fläche.
- Berechnen Sie das von dieser Fläche und der Ebene $x=1$ begrenzte Volumen.
Tipp
Rotiert eine Funktion $g(x)$ um die $x$-Achse, gilt für die dabei entstehende Rotationsfläche $F$
$\D F = 2\pi \int_a^b g(x) \sqrt{1+(g'(x))^2} \, dx$.
Führe anschließend eine Substitution durch, um das Integral zu berechnen.
Lösung
Aufgabenteil 1
Für die Rotationsfläche gilt: $\D F = 2 \pi \int_a^b\,g(x)\,\sqrt{1+(g'(x)^2)}\,dx$
mit $g(x) = x^3$ und $g'(x) = 3x^2$ folgt:
$\begin{align}
F
&= \D 2\pi \int_0^1 \,x^3\,\sqrt{1+(3x^2)^2}\,dx \\
\end{align}$
Wir substituieren: $\D u = 1+(3x^2)^2 \quad \LR \quad 36x^3\,dx = du \quad \LR \quad dx = \frac{1}{36x^3} du \quad$ (Achtung: Integrationsgrenzen verändern sich mit der Substituion!)
$\begin{align}
\D F
&= 2 \pi \int_1^{10} \frac{1}{36x^3} x^3 \sqrt{u}\,du \\
\\
&= \frac{2}{36} \pi \int_1^{10} \sqrt{u}\, du = \D \frac{2}{36} \pi \;\frac{2 u^{\frac{3}{2}}}{3} \Bigg|_1^{10} \\
\\
&= \frac{4\pi}{3 \cdot 36} \Big[10^{\frac{3}{2}} - 1^{ \frac{3}{2}}]
= \frac{\pi}{27} \Big[10^{\frac{3}{2}} - 1] \approx 3.56
\end{align}$
Aufgabenteil 2
Für das Rotationsvolumen gilt allgemein: $\D V = \pi \int_a^b (g(x))^2\,dx$.
Mit $\D g(x) = x^3$ folgt also:
$\begin{align} \D
V = \pi \int_0^1 x^6\,dx = \frac{\pi}{7}
\end{align}$
Aufgabe 5
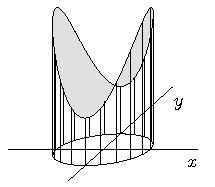
- Berechnen Sie den Flächeninhalt des Teils des durch $z=2+x^2-y^2$ beschriebenen Hyperboloids, der oberhalb
des durch $x^2+y^2\le 1$ beschriebenen Kreises in der $x$-$y$-Ebene liegt.
- Berechnen Sie das Volumen des Körpers, der zwischen Kreis und und Fläche liegt.
Tipp
Führe Zylinderkoordinanten ein, um die Integrale zu berechnen.
Lösung
Beschreibung der Fläche $F$
$F(x,y) = \V{x \\ y \\ 2+x^2-y^2}$ mit $x^2+y^2 \le 1$
$F_x \times F_y = \V{1 \\ 0 \\ 2x} \times \V{0 \\ 1 \\ -2y} = \V{-2x \\ 2y \\ 1}$
$|| F_x \times F_y || = \sqrt{1+4x^2+4y^2}$
Berechnung des Flächeninhaltes
Unter Verwendung von Zylinderkoordinanten:
$\begin{array}{rcll}
&\D \int_{x^2+y^2 \le 1} \sqrt{1+4x^2+4y^2} d(x,y) &= &\D \int_{t=0}^{2\pi} \int_{r=0}^{1} \sqrt{1+4r^2}r\,dr dt & \\
& &= &\D 2\pi \frac{1}{12} \left[ (1+4r^2)^{\frac{3}{2}} \right]_0^1 & \\
& &= &\D \frac{\pi}{6} (5^{\frac{3}{2}}-1) &
\end{array}$
Berechnung des Volumens
$\begin{align}
\D V
&= \D \int_{x^2+y^2 \le 1} (2+x^2-y^2)\,d(x,y) \\
&= \D \int_{r=0}^{1} \int_{t=0}^{2\pi} (2+r^2 \cos^2t-r^2 \sin^2 t)r\,dt dr \\
&= \D \int_{t=0}^{2\pi} \left[ r^2+\frac{1}{3}r^2(\cos^2 t - \sin^2 t) \right]_{r=0}^{r=1}\,dt \\
&= \D \int_{t=0}^{2\pi} (1+\frac{1}{3} (\underbrace{\cos^2t-\sin^2t}_{\cos 2t}) dt \\
&= \D \left[ t + \frac{1}{6} \sin 2t \right]_0^{2\pi} = 2 \pi
\end{align}$