Aufgabe 1
- Beschreiben Sie die folgende Menge in kartesischen und in Polarkoordinaten:
- Berechnen Sie den Schwerpunkt.
Tipp
Eine Kreisgleichung in kartesischen Koordinanten lautet z.B. (hier Kreis in x-y-Ebene mit Radius 3): $x^2+y^2=9$.
Nutze die Symmetrie der Menge.
Nutze die Symmetrie der Menge.
Lösung
Polarkoordinanten
${\D M_P := {(r, \varphi) \in \bbbr^2\,|\, 2 \le r \le 3, \frac{\pi}{2} \le \varphi \le 2\pi}}$
Kartesische Koordinaten
Hierzu wird die Fläche in vier Teile zerlegt.
${\D \begin{align} -3 \le& x \le -2,& -\sqrt{9-x^2} \le& y \le \sqrt{9-x^2} \\ \\ -2 \le& x \le 0,& \sqrt{4-x^2} \le& y \le \sqrt{9-x^2} \\ \\ -2 \le& x \le 2,& -\sqrt{9-x^2} \le& y \le -\sqrt{4-x^2} \\ \\ 2 \le& x \le 3,& -\sqrt{9-x^2} \le& y \le 0 \end{align}}$
Berechnung des Schwerpunktes
Zunächst wird die Fläche $A$ des Kreises bestimmt.
$A={\D \int_2^3 \int_{ \frac{\pi}{2}}^{2\pi} r \, d\varphi dr = \frac{3}{2} \pi \Big[ \frac{r^2}{2} \Big]_2^3=\frac{3}{2} \pi \left( \frac{9}{2} - 2 \right) = \frac{15}{4} \pi} $
Für den Schwerpunkt gilt $\vec{S}=\V{S_x \\ S_y}$. Aus Symmetriegründen (Kreis) folgt: $S_x = S_y$
$\D S_x = \frac{4}{15\pi} \pi \int_2^3 \int_{\frac{\pi}{2}}^{2 \pi} r \cos\varphi\;r\;d\varphi dr = \frac{4}{15\pi} {\D \Big[ \sin\varphi \Big]_{\frac{\pi}{2}}^{2\pi}} \, {\D \Big[ \frac{r^3}{3} \Big]_2^3} = \frac{4}{15\pi} (0-1)(9-\frac{8}{3}) = -\frac{76}{45\pi}$
Somit lautet der Schwerpunkt: $\D \vec{S} = \D \V{\D -\frac{76}{45\pi} \\ \D -\frac{76}{45\pi}}$
${\D M_P := {(r, \varphi) \in \bbbr^2\,|\, 2 \le r \le 3, \frac{\pi}{2} \le \varphi \le 2\pi}}$
Kartesische Koordinaten
Hierzu wird die Fläche in vier Teile zerlegt.
${\D \begin{align} -3 \le& x \le -2,& -\sqrt{9-x^2} \le& y \le \sqrt{9-x^2} \\ \\ -2 \le& x \le 0,& \sqrt{4-x^2} \le& y \le \sqrt{9-x^2} \\ \\ -2 \le& x \le 2,& -\sqrt{9-x^2} \le& y \le -\sqrt{4-x^2} \\ \\ 2 \le& x \le 3,& -\sqrt{9-x^2} \le& y \le 0 \end{align}}$
Berechnung des Schwerpunktes
Zunächst wird die Fläche $A$ des Kreises bestimmt.
$A={\D \int_2^3 \int_{ \frac{\pi}{2}}^{2\pi} r \, d\varphi dr = \frac{3}{2} \pi \Big[ \frac{r^2}{2} \Big]_2^3=\frac{3}{2} \pi \left( \frac{9}{2} - 2 \right) = \frac{15}{4} \pi} $
Für den Schwerpunkt gilt $\vec{S}=\V{S_x \\ S_y}$. Aus Symmetriegründen (Kreis) folgt: $S_x = S_y$
$\D S_x = \frac{4}{15\pi} \pi \int_2^3 \int_{\frac{\pi}{2}}^{2 \pi} r \cos\varphi\;r\;d\varphi dr = \frac{4}{15\pi} {\D \Big[ \sin\varphi \Big]_{\frac{\pi}{2}}^{2\pi}} \, {\D \Big[ \frac{r^3}{3} \Big]_2^3} = \frac{4}{15\pi} (0-1)(9-\frac{8}{3}) = -\frac{76}{45\pi}$
Somit lautet der Schwerpunkt: $\D \vec{S} = \D \V{\D -\frac{76}{45\pi} \\ \D -\frac{76}{45\pi}}$
Aufgabe 2
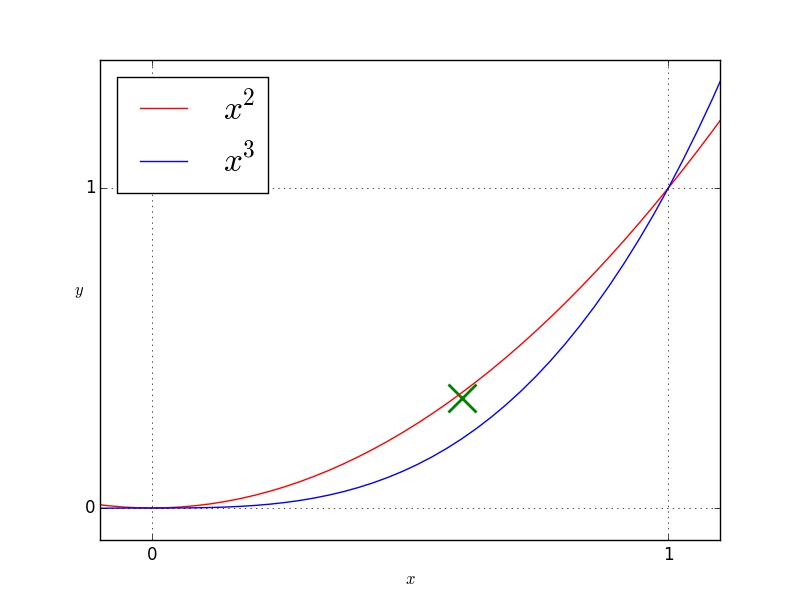
Die Fläche $B$ sei der von den Graphen von $y=x^2$ und $y=x^3$ umschlossene Bereich zwischen den Schnittpunkten.Berechnen Sie den Schwerpunkt und weisen Sie nach, dass er innerhalb von B liegt.
Tipp
- Skizziere die Fläche!
- Bestimme, welche Funktion den oberen Rand definiert und welche den unteren Rand definiert.
- An welchen zwei Punkten schneiden sich die Funktionen?
- Wähle anhand dieser Informationen die Integrationsgrenzen für die Flächenberechnung.
Lösung
Integrationsgrenzen
Die Schnittpunkte der Kurven, die die Fläche begrenzen lauten: $(0,0)$ und $(1,1)$.
In diesem Intervall wächst $x^3$ langsamer und liegt deshalb unterhalb von $x^2$.
Berechne Fläche B
$B = \D \int_0^1 (x^2-x^3)\,dx=\frac{1}{3} - \frac{1}{4} = \frac{1}{12}$
Berechne Schwerpunkt
Für den Schwerpunkt gilt allgemein: $\vec{S} = \V{S_x \\ S_y}$
$\D S_x = 12 \int_0^1 \int_{x^3}^{x^2}\,x\,dydx=12 \int_0^1 (x^3-x^4)\,dx $ $= \D 12 (\frac{1}{4} - \frac{1}{5}) = \frac{12}{20} = \frac{3}{5} $
$\D S_y = 12 \int_0^1 \int_{x^3}^{x^2}\,y\;dydx=12 \int_0^1 \Big[ \frac{y^2}{2}\Big]_{x^3}^{x^2}\,dx = 6 \int_0^1 (x^4-x^6)\,dx = 6 (\frac{1}{5} - \frac{1}{7}) = \frac{12}{35}$
Somit ist $\vec{S} = \V{\D \frac{3}{5} \\ \D \frac{12}{35}}$
Nachweis, dass der Schwerpunkt innerhalb von B liegt
Es sei $f_1(x):=x^2$ und $f_2(x):=x^3$.
$\D f_2(S_x)=f_2(\frac{3}{5})=\frac{27}{125}=\frac{189}{875} < \frac{270}{875} = \frac{12}{35} < (\frac{3}{5})^2 = f_1(\frac{3}{5}) = f_1(S_x)$
$\D f_1(S_x)=f_1(\frac{3}{5})=(\frac{3}{5})^2=\frac{9}{25}=\frac{63}{175} > \frac{60}{175} = \frac{12}{35}$
(Klicken zum Vergrößern)
Die Schnittpunkte der Kurven, die die Fläche begrenzen lauten: $(0,0)$ und $(1,1)$.
In diesem Intervall wächst $x^3$ langsamer und liegt deshalb unterhalb von $x^2$.
Berechne Fläche B
$B = \D \int_0^1 (x^2-x^3)\,dx=\frac{1}{3} - \frac{1}{4} = \frac{1}{12}$
Berechne Schwerpunkt
Für den Schwerpunkt gilt allgemein: $\vec{S} = \V{S_x \\ S_y}$
$\D S_x = 12 \int_0^1 \int_{x^3}^{x^2}\,x\,dydx=12 \int_0^1 (x^3-x^4)\,dx $ $= \D 12 (\frac{1}{4} - \frac{1}{5}) = \frac{12}{20} = \frac{3}{5} $
$\D S_y = 12 \int_0^1 \int_{x^3}^{x^2}\,y\;dydx=12 \int_0^1 \Big[ \frac{y^2}{2}\Big]_{x^3}^{x^2}\,dx = 6 \int_0^1 (x^4-x^6)\,dx = 6 (\frac{1}{5} - \frac{1}{7}) = \frac{12}{35}$
Somit ist $\vec{S} = \V{\D \frac{3}{5} \\ \D \frac{12}{35}}$
Nachweis, dass der Schwerpunkt innerhalb von B liegt
Es sei $f_1(x):=x^2$ und $f_2(x):=x^3$.
$\D f_2(S_x)=f_2(\frac{3}{5})=\frac{27}{125}=\frac{189}{875} < \frac{270}{875} = \frac{12}{35} < (\frac{3}{5})^2 = f_1(\frac{3}{5}) = f_1(S_x)$
$\D f_1(S_x)=f_1(\frac{3}{5})=(\frac{3}{5})^2=\frac{9}{25}=\frac{63}{175} > \frac{60}{175} = \frac{12}{35}$

(Klicken zum Vergrößern)
Aufgabe 3
Sei $G$ der Teil des Paraboloids $\{ (x,y,z)\,|\, x^2+y^2\le z\}$ mit $x\ge 0$, $y\ge 0$ und $0\le z\le 2$.Berechnen Sie die Koordinaten des Schwerpunkts von $G$, wenn die Massendichte durch $\mu(x,y,z)=x$ gegeben ist.
Tipp
- Wähle geeignete Koordinaten.
- Jacobi-Determinante nicht vergessen!
- Bedenke, dass $x \ge 0$ und $y \ge 0$ gilt. In welchem Quadranten der x-y-Ebene liegt die Figur? Was bedeutet dies für die Integrationsgrenzen des Winkels?
Lösung
Wähle Zylinderkoordinaten
$\V{x \\ y \\ z} := \V{r \cos\rho \\ r\sin\rho \\ z} \qquad$ für $\rho$, $z$ und $r$ gilt: $\begin{align} 0 \le& \rho \le \frac{\pi}{2} \\ 0 \le& z \le 2 \\ 0 \le& r \le \sqrt{z} \end{align}$
(Achtung: Jacobi-Determinante für die gewählten Koordinanten nicht vergessen!)
Berechnung der Masse
$\D M = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \underbrace{r \cos \rho}_{\mu(x,y,z) = x}\,r\,d\rho dr dz = \int_{z=0}^2 \left[ \frac{r^3}{3} \right]_0^{\sqrt{3}} dz = \frac{1}{3} \int_{z=0}^2 z^{\frac{3}{2}} dz = \frac{2}{15} \left[ z^{\frac{5}{2}} \right]_0^2 = \frac{2}{15} \sqrt{2}^5 = \frac{8 \sqrt{2}}{15}$
Berechne Schwerpunkt
Für den Schwerpunkt $\vec{S}$ gilt: $\vec{S}=\V{S_x \\ S_y \\ S_z}$.
$\D M\,S_x = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \underbrace{r \cos\rho}_{x}\,\underbrace{r\cos\rho}_{\mu=x}\,r\,d\rho dr dz = \int_{z=0}^2 \left[ \frac{r^4}{4} \right]_0^{\sqrt{z}} \underbrace{\int_{\rho=0}^{\frac{\pi}{2}} \cos^2 \rho\, d\rho}_{\frac{\pi}{4}} = \frac{\pi}{16} \int_{z=0}^2 z^2\,dz=\frac{\pi}{16} \frac{8}{3} = \frac{\pi}{6}$
Somit ist $\D S_x = \frac{15}{8 \sqrt{2}} \frac{\pi}{6} = \frac{5 \sqrt{2} \pi}{32}$
$\D M\,S_y = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} r\sin\rho\, r\cos\rho\,r\,d\rho dr dz = \int_{z=0}^{2} \left[ \frac{r^4}{4} \right]_0^{\sqrt{z}} dz \underbrace{\int_{\rho=0}^{\frac{\pi}{2}} \sin\rho\cos\rho\,d\rho}_{\frac{1}{2}} = \frac{1}{8} \int_{z=0}^{2} z^2 dz = \frac{8}{24} = \frac{1}{3}$
Somit ist $\D S_y = \frac{15}{8\sqrt{2}} \frac{1}{3} = \frac{5 \sqrt{2}}{16}$
$\D M\,S_z = \int_{z=0}^{2} \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} z\,r\cos\rho\,r\,d\rho dr dz = \int_{z=0}^{2} \left[ \frac{r^3}{3} \right]_0^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \cos\rho d\rho = \frac{1}{3} \int_{z=0}^{2} z^{\frac{5}{2}}\,dz = \frac{2}{21} \left[ z^{\frac{7}{2}} \right]_0^2 = \frac{16}{21} \sqrt{2}$
Somit ist $\D S_z = \frac{16}{21} \sqrt{2} \frac{15}{8 \sqrt{2}} = \frac{30}{21} = \frac{10}{7}$
Insgesamt also: $\vec{S} = \V{\frac{5 \sqrt{2} \pi}{32} \\ \frac{5 \sqrt{2}}{16} \\ \frac{10}{7}}$
$\V{x \\ y \\ z} := \V{r \cos\rho \\ r\sin\rho \\ z} \qquad$ für $\rho$, $z$ und $r$ gilt: $\begin{align} 0 \le& \rho \le \frac{\pi}{2} \\ 0 \le& z \le 2 \\ 0 \le& r \le \sqrt{z} \end{align}$
(Achtung: Jacobi-Determinante für die gewählten Koordinanten nicht vergessen!)
Berechnung der Masse
$\D M = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \underbrace{r \cos \rho}_{\mu(x,y,z) = x}\,r\,d\rho dr dz = \int_{z=0}^2 \left[ \frac{r^3}{3} \right]_0^{\sqrt{3}} dz = \frac{1}{3} \int_{z=0}^2 z^{\frac{3}{2}} dz = \frac{2}{15} \left[ z^{\frac{5}{2}} \right]_0^2 = \frac{2}{15} \sqrt{2}^5 = \frac{8 \sqrt{2}}{15}$
Berechne Schwerpunkt
Für den Schwerpunkt $\vec{S}$ gilt: $\vec{S}=\V{S_x \\ S_y \\ S_z}$.
$\D M\,S_x = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \underbrace{r \cos\rho}_{x}\,\underbrace{r\cos\rho}_{\mu=x}\,r\,d\rho dr dz = \int_{z=0}^2 \left[ \frac{r^4}{4} \right]_0^{\sqrt{z}} \underbrace{\int_{\rho=0}^{\frac{\pi}{2}} \cos^2 \rho\, d\rho}_{\frac{\pi}{4}} = \frac{\pi}{16} \int_{z=0}^2 z^2\,dz=\frac{\pi}{16} \frac{8}{3} = \frac{\pi}{6}$
Somit ist $\D S_x = \frac{15}{8 \sqrt{2}} \frac{\pi}{6} = \frac{5 \sqrt{2} \pi}{32}$
$\D M\,S_y = \int_{z=0}^2 \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} r\sin\rho\, r\cos\rho\,r\,d\rho dr dz = \int_{z=0}^{2} \left[ \frac{r^4}{4} \right]_0^{\sqrt{z}} dz \underbrace{\int_{\rho=0}^{\frac{\pi}{2}} \sin\rho\cos\rho\,d\rho}_{\frac{1}{2}} = \frac{1}{8} \int_{z=0}^{2} z^2 dz = \frac{8}{24} = \frac{1}{3}$
Somit ist $\D S_y = \frac{15}{8\sqrt{2}} \frac{1}{3} = \frac{5 \sqrt{2}}{16}$
$\D M\,S_z = \int_{z=0}^{2} \int_{r=0}^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} z\,r\cos\rho\,r\,d\rho dr dz = \int_{z=0}^{2} \left[ \frac{r^3}{3} \right]_0^{\sqrt{z}} \int_{\rho=0}^{\frac{\pi}{2}} \cos\rho d\rho = \frac{1}{3} \int_{z=0}^{2} z^{\frac{5}{2}}\,dz = \frac{2}{21} \left[ z^{\frac{7}{2}} \right]_0^2 = \frac{16}{21} \sqrt{2}$
Somit ist $\D S_z = \frac{16}{21} \sqrt{2} \frac{15}{8 \sqrt{2}} = \frac{30}{21} = \frac{10}{7}$
Insgesamt also: $\vec{S} = \V{\frac{5 \sqrt{2} \pi}{32} \\ \frac{5 \sqrt{2}}{16} \\ \frac{10}{7}}$