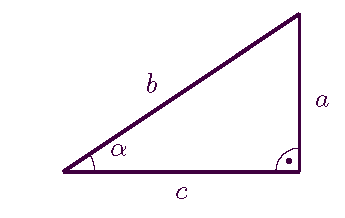
In einem rechtwinkligen Dreieck ist der Sinus des Winkels $\alpha$ das Verhältnis der Seiten $a$ und $b$ (Gegenkathete:Hypothenuse), also $\displaystyle \sin \alpha=\frac{a}{b}$.
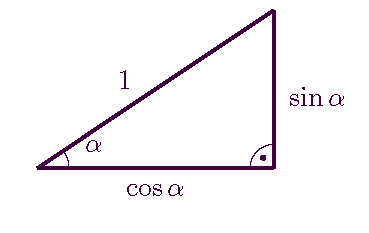
Hat die Hypothenuse die Länge $1$, so ist der Sinus die Länge der Gegenkathete $a$.
Genauso ist der Cosinus von $\alpha$ das Verhältnis von $c$ und $b$ (Ankathete:Hypothenuse)), also $\displaystyle \cos \alpha=\frac{c}{b}$. Bei Hypothenusenlänge $1$ der Cosinus die Länge der Ankathete $c$.

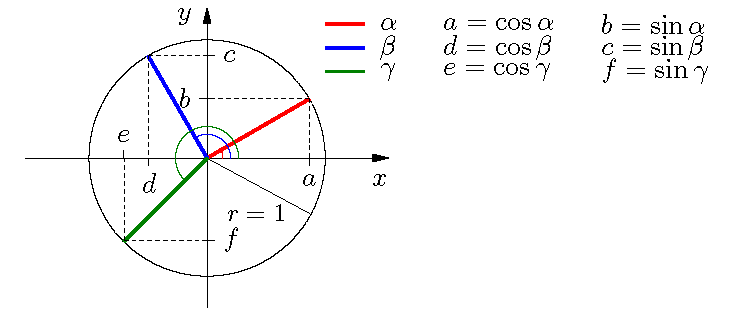
Allgemein ist der Cosinus eines Winkels $\alpha$ die $x$-Koordinate des Punktes auf einem Kreis um $(0,0)$ mit Radius $1$, dessen Verbindungsstrecke mit dem Ursprung mit der $x$-Achse den Winkel $\alpha$ einschließt, der Sinus die entsprechende $y$-Koordinate.

Wichtige Werte und Eselsbrücke $\displaystyle \begin{array}{r|ccccc} \text{Winkel} & 0^\circ & 30^\circ & 45^\circ & 60^\circ & 90^\circ\\ & 0 & \frac{\pi}{6}&\frac{\pi}{4}& \frac{\pi}{3} & \frac{\pi}{2} \\ \sin \alpha & 0 & \frac{1}{2} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{2} & 1\\ \text{Eselsbrücke}& \frac{\sqrt{0}}{1} & \frac{\sqrt{1}}{2} & \frac{\sqrt{2}}{2}& \frac{\sqrt{3}}{2} & \frac{\sqrt{4}}{2} \\ \cos \alpha & 1 & \frac{\sqrt{3}}{2} & \frac{\sqrt{2}}{2} & \frac{1}{2} & 0 \end{array} $

Werte in anderen Winkelbereichen

Die Werte der trigonometrischen Funktionen in anderen Winkelbereichen können auf die Werte für Winkel im Intervall $[0,\pi/2]$ zurückgeführt werden:
$\displaystyle \begin{array}{ll} \sin (\alpha+\pi/2) &=\cos \alpha \\ \cos (\alpha+\pi/2) &=-\sin \alpha \\ \sin (\alpha+\pi) &=-\sin \alpha\\ \cos (\alpha+\pi) &=-\cos \alpha\\ \end{array} $
Weiter ist $\sin (-\alpha)=-\sin \alpha$ und $\cos (-\alpha)=\cos \alpha$.
Für eine ganze Zahl $k$ ist allgemein $\sin (\alpha+k\pi)=(-1)^k \sin \alpha$ und $\cos(\alpha+k\pi)=(-1)^k \cos \alpha$.
$(-1)^k=1$, wenn $k$ gerade ist und $(-1)^k=-1$, wenn $k$ ungerade ist.

Immer ist $(\sin \alpha)^2+(\cos \alpha)^2=1$.

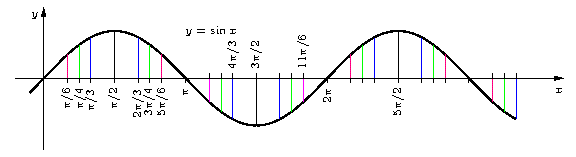
Alle Werte von Sinus und Cosinus kommen (mit möglicherweise anderem Vorzeichen) zwischen $0$ und $\frac{\pi}{2}$ vor. Graph der Sinusfunktion: