Hinweise zu den Verallgemeinerungen
Derive kann auch mit einer beliebigen Funktion f(x)
arbeiten. Dazu definiert man eine unbelegte Funktion durch f(x):=
Weiter werden nun Funktionen definiert, die mehrere Variable benutzen. Die Variablen sind a, als linke Grenze, b als rechte Grenze und n als Anzahl der Teilintervalle.
Die Flächenberechnung erfolgt durch
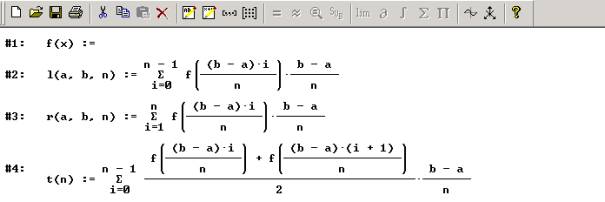
Wenn Sie Hilfen zur Summenbildung benötigen, klicken Sie bitte hier
Nun lässt sich für jedes f(x) , jedes Intervall [a,b] in n Teile zerlegen und die Fläche berechnen. Z:B: für f(x)=x2

Bildet man die Grenzwerte, so zeigt sich, dass alle Funktionen zum selben Wert führen.

Wenn Sie Hilfen zur Grenzwertbildung benötigen, klicken Sie bitte hier
Die Stärke von Derive zeigt sich hier, wenn man die Variablengrenzen variabel hält.

Gleiches gilt auch für die anderen Berechnungsmöglichkeiten.
Es lohnt sich für den weiteren Verlauf, diese Berechnungen unter einem bestimmten Namen zu definieren

Man „sieht“ schon den Hauptsatz der Differenzial- und Integralrechnung.
Versuchen Sie es selbst eigener Versuch Schließen Sie abschließend das Derivefenster.
8