Weiterführung

zurück zur Einführung

Spätestens hier ist es ratsam, das Einführungsbeispiel zu verlassen und sich mit einfacheren Funktionen zu befassen, damit die SchülerInnen den Zusammenhang zwischen Flächenberechnung und Integral und dem Hauptsatz der Differential- und Integralrechnung selber finden können.

Wir betrachten die Funktion f(x)=x³-4x²+4x+1 im Intervall I=[0,3] und berechnen die Fläche (durch Rechtecke, deren Höhe durch den Funktionswert an der linken Teilintervallgrenze festgelegt wird) zwischen der x-Achse und dem Graphen von f.

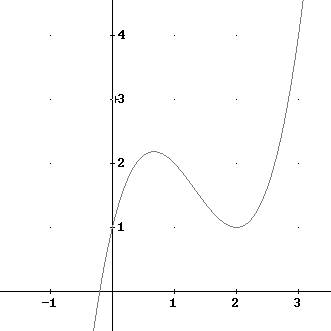
Aufgabe:

Berechnen Sie die Fläche zwischen dem Graphen von f(x) und der x-Achse im Intervall [0,3]

Entwickeln Sie für diese Funktion auch eine allgemeine Formel zur Flächenberechnung der Fläche zwischen dem Graphen von f(x) und der x-Achse im Intervall [0,b] und anschließend im Intervall [a,b]

Sie können direkt mit eigener Versuch die Aufgabe bearbeiten oder sich Hilfe holen unter Hilfen zur Flächenberechnung

Wer gerne mit Veranschaulichungen arbeitet, kann hier mit Erfolg die Datei

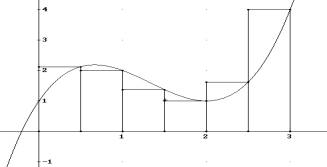
Integralstufen einsetzen.

Aufgabe :

Arbeiten Sie mit der Datei Treppenstufen Integral 1.dfw und zeichnen Sie zu verschiedenen Funktionen, die entsprechenden Rechtecke oder Trapeze.

Wir kehren wieder zur Flächenberechnung zurück und verallgemeinern.

Aufgabe:

Führen Sie eine Verallgemeinerung für beliebiges f(x), ein beliebiges Intervall durch.

Führen Sie die Verallgemeinerung auch für Rechtecke durch, deren Höhe durch die linke Teilintervallgrenze vorgegeben wird. Ebenso für Trapezausschöpfungen.

Hinweise zu den Verallgemeinerungen

Durch mehrere Beispiele lässt sich schon hier ein Zusammenhang zwischen der Integralfunktion und der Integrandenfunktion von den SchülerInnen selbstständig finden. An dieser Stelle kann dann auch der Hauptsatz der Differential- und Integralrechnung verbalisiert werden (Beweis folgt erst später)

Bis hierhin gleicht die Berechnung unserem Amalgambeispiel. Was aber passiert, wenn wir die Fläche zwischen dem Graphen von f(x)=x³-4x²+4x-0.75 wiederum im Intervall [0,3] und der a-Achse berechnen wollen?

Aufgabe:

Probieren Sie selbst!

Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derivefenster.

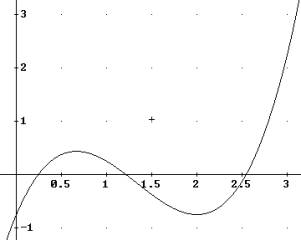
Wie ist dieses Ergebnis ( das Resultat ist 0) zu erklären?

Schauen wir uns den berechneten Term genauer an, so erkennen wir, dass einige Summanden negativ sind, da der Graph von f(x) die x-Achse schneidet und damit die Funktionswerte negativ werden. Es werden hier sowohl positive als auch negative „Flächenmaße“ berechnet. Wir nennen solche Maßzahlen „orientierte Flächenmaße“.

Unsere Rechenterme ermitteln die Summe der orientierten Flächeninhalt im Intervall [0,a].

Hierfür verwenden wir von nun an den Begriff Integral.

Definition: linkeSumme=rechteSumme=Trapezsumme=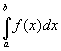

(sprich: “Integral von f(x) dx in den Grenzen von a bis b“)

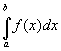berechnet also nur dann das Flächenmaß zwischen dem Graphen von f(x) und der x-Achse im Intervall [a,b], wenn die Funktion nur positive Funktionswerte besitzt.

Wie berechnen wir dann das Flächenmaß, wenn die Funktion auch negative Funktionswerte hat?

Hinweise zur Flächenberechnung von Flächen oberhalb und unterhalb der x-Achse finden Sie hier

Aufgabe:

Probieren Sie selbst!

Das Flächenmaß zwischen der x-Achse und dem Graphen einer Funktion f(x) im Intervall [a,b] berechnet man:

· Durch Integration von f(x) jeweils zwischen den Nullstellen im Intervall [a,b] und anschließender Addition der Absolutbeträge der Teile

Oder

· Durch Integration des Absolutbetrages von f(x) im Intervall [0,a]

Berechnung der Fläche zwischen den Graphen zweier Funktionen

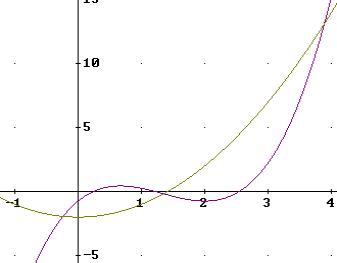
Es soll die Fläche zwischen den beiden Funktionsgraphen von f(x)= - 4x² + 4x - 0.75 und g(x)=x² – 2 berechnet werden.

Aufgabe:

Stellen Sie eigene Überlegungen und Berechnungen an.

Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derivefenster.

Berechnen Sie auch die Fläche zwischen den Graphen zweier Funktionen, die sich in mehr als zwei Stellen schneiden.

Beispiel: f(x)= x³ – 4x² + 4x –0.75 und g(x) = x² - 2

Das Flächenmaß zwischen den Graphen zweier Funktionen berechnet man:

· Durch Integration der Differenzfunktion jeweils zwischen den Schnittstellen der Funktionen und anschließender Addition der Absolutbeträge der Teile

Oder

· Durch Integration des Absolutbetrags der Differenzfunktion zwischen der kleinsten und der größten Schnittstelle.

Aufgabe:

Führen Sie die Berechnungen durch

Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derivefenster.

Hier kann der Beweis des Hauptsatzes das Kapitel abschließen.