In the univariate case the zeros of Jacobi-polynomials give Gauss-Jacobi quadratures which are distinguished by highest possible degree of exactness. Moreover, these quadratures have positive weights from which convergence of these formulae is guaranteed.
To advance to the multivariate case, an interpretation of the zeros of the
Jacobi polynomials is helpful. The zeros of these orthogonal polynomials are
closely connected to movable charges situated on a metal rod which is
represented by the real interval 
.
In the state of equilibrium the potential energy of the charge distribution
is minimized and their locations coincide with the zeros of the Jacobi
polynomials. For more details see Stroud and Secrest [24, p. 17,].
Thus a minimization of the potential energy of a point distribution on the sphere is a good criterion for an appropriate node distribution.
With 
the Euclidian norm in 
we get for
electrical charged point particles at locations 
the potential energy
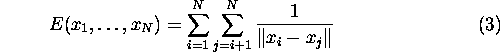
and thus the nonlinear optimization problem
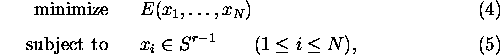
which is a facility dispersion problem on the sphere.
In computational physics and chemistry, this problem is also known as
Thomson's problem.