In the cases where the calculated nodes can be shown to be spherical designs (N=2,4,6,12), equal weights are optimal. This can be seen with the aid of Theorems 3 and 4. In all other cases appropriate weights have to be calculated.
With the aid of multivariate interpolation theory this is at least possible
if the number N of nodes equals the dimension of the linear
space of polynomials ![]() . For r=3 this means that
. For r=3 this means that
![]() .
.
Let ![]() and let
and let ![]() be the symmetric matrix being
composed of the evaluation of the kernel
be the symmetric matrix being
composed of the evaluation of the kernel ![]() at the nodes
at the nodes ![]() ,
,
![]() .
.
If ![]() are a fundamental system,
i. e.
are a fundamental system,
i. e. ![]() , then the interpolation property
, then the interpolation property
![]()
and the following consequence of the reproducing property of ![]()
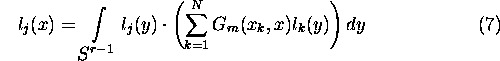
are valid.
Here, ![]() denote the Lagrange fundamental polynomials.
Equations (6) and (7) lead to
denote the Lagrange fundamental polynomials.
Equations (6) and (7) lead to
![]()
which means that the matrices ![]() and
and ![]() are inverse to each other.
are inverse to each other.
Consider now a cubature formula
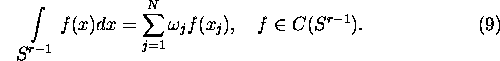
The function f can be substituted in the usual way by its
interpolation polynomial p with regard to the nodes ![]() . Then
. Then
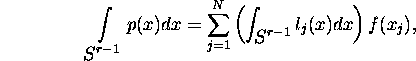
that is
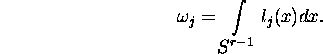
Because ![]() and
and ![]() this yields
this yields
![]()
which is the row-sum of the matrix L.
Thus, because of (1), the weights of the cubature formula can be
computed as the row-sum of the symmetric matrix
![]()
The Gegenbauer polynomials of degree m with index r/2 occuring
in this composition have the representation
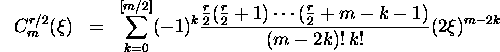
with ![]() .
.
They can be evaluated with the aid of their recurrence relation (see
e. g. Reimer [16])
![]()
The inversion of the matrix ![]() can be avoided.
With
can be avoided.
With
![]()
we obtain the vector ![]() of
weights as solution of the linear system of equations
of
weights as solution of the linear system of equations
![]()
In the following, we study the case r=3, that is ![]() , in detail,
but the theory can be extended to higher
dimensions without any difficulties.
, in detail,
but the theory can be extended to higher
dimensions without any difficulties.
The cases ![]() cannot be handled yet except for those cases in
which the nodes are spherical designs.
These are the cases N = 2,4,6,12 . The weights then can be chosen to be
cannot be handled yet except for those cases in
which the nodes are spherical designs.
These are the cases N = 2,4,6,12 . The weights then can be chosen to be
![]() .
The cases N=3,5,7 also show a regular behaviour, but up to now it could
not be decided if these nodes are spherical designs.
As interpolatory formulae our cubatures have a degree of exactness
equal to m, whereas the spherical designs yield a degree of exactness
equal to 2m or 2m+1, respectively.
.
The cases N=3,5,7 also show a regular behaviour, but up to now it could
not be decided if these nodes are spherical designs.
As interpolatory formulae our cubatures have a degree of exactness
equal to m, whereas the spherical designs yield a degree of exactness
equal to 2m or 2m+1, respectively.