Literatur

Ai96

M. Ainsworth: The influence and selection of subspaces for a posteriori error estimators, Numer. Math. 73, No. 4, 399-418 (1996)

Ai97

M. Ainsworth, B. Senior, D. Andrews: Preconditioners for the adaptive 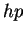$hp$ version finite element method, in: Whiteman, J.R.: The mathematics of finite elements and applications. Highlights 1996. Proceedings of the 9th conference, MAFELAP 1996, Uxbridge, GB, June 25-28, 1996, Chichester: Wiley, 81-96 (1997).

Ba78

I. Babuska, W. Rheinboldt: Error estimates for adaptive finite element computations, SIAM J. Numer. Anal. 15, 736-754 (1978)

Ba94

I. Babuska, M. Suri: The p- and h-p-versions of the finite element method, basic principles and properties, SIAM Review, Vol. 36, No. 4, pp. 578-632, 1994

Ba85

R.E. Bank, A. Weiser: Some a posteriori error estimators for elliptic partial differential equations, Math. Comp. 44, 283-301 (1985)

Be96

R. Becker, R. Rannacher: A feed-back approach to error control in finite element methods: Basic analysis and examples, East-West J. Numer. Math. 4, 237-264 (1996).

Bl88

H. Blum: Numerical treatment of corner and crack singularities, in: E.Stein, W.L. Wendland (Hrsg.): FEM and BEM Techniques from Mathematical and Engineering Point of View, CISM Courses and Lectures No. 301, Springer-Verlag, Wien-New-York, 1988

Bl92

H. Blum, J. Harig, S. Müller, S. Turek:FEAT2D. Finite element analysis tools. User manual. Release 1.3. Preprint 1992-18, Universität Heidelberg, 1992.

Bl97

H. Blum, A. Langer, A. Schröder: LiMA - An Object Oriented Approach to Mesh Representation in 2D/3D, Universität Dortmund, Ergebnisberichte Angewandte Mathematik Nr. 155-T, 1997.

Bl98

H. Blum, A. Langer, A. Schröder: LiMA - A Generic Class Library for Mesh Representation in 2D/3D, erscheint in ,,Notes on Numerical Fluid Mechanics``, Proceedings of the 14th GAMM Seminar Kiel on Concepts of Numerical Software, Kiel 1998.

Bl99

H. Blum, St. Wilkes: Semiimplicit Galerkin methods for initial value problems, in Vorbereitung

Ca98

C. Carstensen, O. Scherf, P. Wriggers: Adaptive finite elements for elastic bodies in contact, Preprint, Univ. Kiel (1998)

Do92

M. Dobrowolski, T. Staib: On finite element approximation of a second order unilateral variational inequality, Numer. Funct. Anal. and Optimiz. 13, 243-247 (1992)

Ek76

I. Ekeland, R. Temam: Convex analysis and variational problems, North Holland 1976

Er95

K. Eriksson, D. Estep, P. Hansbo, C. Johnson: Introduction to adaptive methods for partial differential equations, Acta Numerica, 105-159 (1995)

Er96

K. Eriksson, D. Estep, P. Hansbo, C. Johnson: Computational Differential Equations, Studentlitteratur, Lund (Schweden) 1996

Gl80

R. Glowinski: Lectures on numerical methods for non-linear variational problems, Tata Lectures 1980

Gl83

R. Glowinski: Numerical methods for nonlinear variational problems, Springer Series in Comp. Physics, Springer 1983

Ha84

W. Hackbusch: Local defect correction method and domain decomposition techniques, Computing Suppl. 5, 89-113 (1984)

Ha94

J. Harig, P. Schreiber, S. Turek: FEAT3D - Finite Element Analysis Tools in 3 Dimensions. User Manual. Release 1.2. Preprint1994-19, Universität Heidelberg, 1994.

Ki88

N. Kikuchi, J.T. Oden: Contact Problems in Elasticity: A Study of Variational Inequalities and Finite Element Methods, SIAM Studies in Applied Mathematics 8

Ki80

D. Kinderlehrer, G. Stampacchia: An introduction to variational inequalities and their applications, Academic Press 1980

Os97

M. Ostermann: Numerische Behandlung von Eckensingularitäten mit Gebietszerlegungstechniken, Juni 1997, Diplomarbeit, Fachbereich Mathematik der Universität Dortmund, 1997

Ra95

E. Rank, R. Krause: A multiscale finite-element-method, Comp. and Structures, 1995

Ra97-1

R. Rannacher and F.T. Suttmeier: A feed-back approach to error control in finite element methods: Application to linear elasticity, Comp. Mech. 19, 434-446 (1997).

Ra97-2

R. Rannacher and F.T. Suttmeier: A posteriori error control and mesh adaptation in elasticity and elasto-plasticity, Preprint 97-36, SFB 359, Universität Heidelberg, 1997, Proc. Workshop ``On New Advances in Adaptive Computational Methods in Mechanics``, Cachan, Sept. 17-19, 1997, Elsevier, to appear.

Ra98

R. Rannacher and F.T. Suttmeier: A Posteriori Error Control in Finite Element Methods via Duality Techniques: Application to Perfect Plasticity, Comp. Mech. 21/2, 123-133 (1998).

Ra98-2

R. Rannacher: Error Control in Finite Element Computations, Preprint 98 - 54 (SFB 359) der Universität Heidelberg.

Ra99

R. Rannacher: A posteriori error estimation in least-squares stabilized finite element schemes, Special issue on Advances in Stabilized Methods in Computational Mechanics, Comp. Meth. in Appl. Mech. and Eng., to appear.

Su96

F.-T. Suttmeier: Adaptive Finite Element Approximation of Problems in Elasto-Plasticity Theory, Dissertation, Institut für Angewandte Mathematik, Universität Heidelberg, 1996.

Su98-1

F.T. Suttmeier: On FE-discretisations with least-squares stabilisation: A posteriori error control for the membrane-problem, EAST-WEST J. Numer. Math., Vol.6, No.2, pp.155-165 (1998).

Su98-2

F.T. Suttmeier: An adaptive displacement/pressure finite element scheme for treating incompressibility effects in elasto-plastic materials, Preprint, Inst. f. Angewandte Mathematik, Universität Heidelberg, Juni 1998, eingereicht bei: Numerical Methods for Partial Differential Equations.

Uh98

I. Uhlenbruch: Lokale Defektkorrektur bei singulären Daten, Diplomarbeit, Fachbereich Mathematik der Universität Dortmund, 1998

We94

W.L. Wendland, e.a.: Arbeiten im Rahmen des DFG-Paketantrags ,, Adaptive Finite-Element-Verfahren in der Angewandten Mechanik``, 1994-1999

Wi98

St. Wilkes: Semiimplizite Galerkin-Diskretisierungen für Anfangswertaufgaben, Diplomarbeit, Fachbereich Mathematik der Universität Dortmund, April 1998

Ve94

R. Verfürth: A posteriori error estimation and adaptive mesh-refinement techniques, J. Comp. Appl. Math. 50, 67-83 (1994)

Ve96

R. Verfürth: A review of a posteriori error estimation and adaptive mesh-refinement techniques, Teubner Skripten zur Numerik, B.G. Wiley-Teubner, Stuttgart, 1996.

Zi87

O.C. Zienkiewicz, J.Z. Zhu: A simple error estimator and adaptive procedure for practical engineering analysis, Int. J. Numer. Meth. Eng. 24 (1987)