Computational Details:

"(Regularized) Driven Cavity (I) at low Reynolds number with interior circle"

• rectangular domain of height 3 and width 3
• Dirichlet b.c.'s (parabolic with maximum value of 1) for the u-velocity at the top
• other b.c.'s: zero velocity at fixed walls
• initial condition at t=0: starting from rest
• viscosity parameter: 1/nu=250

• coarse mesh (=level 2): 32 cells, 48 vertices, 192 d.o.f.`s
  

  
  
  

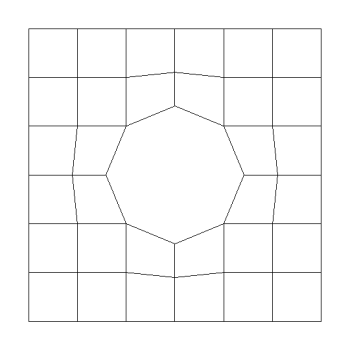
• uniform refinements with exact boundary adaption
• visualization on level 6: 8,192 cells, 8,448 vertices, 41,472 d.o.f.`s
• computational mesh on level 7: 32,768 cells, 33,280 vertices, 164,864 d.o.f.`s
• nonconforming nonparametric rotated bilinear fem's (meanvalue version), UPW

• equidistant time stepping for computation with k=0.083333334
• equidistant time stepping for visualization with k=0.25 (= 1 frame)
• Total time T=100 seconds corresponds to 1,200 time steps
• fractional step theta scheme

• date: 23/6/98
• simulation by: F.Loewner/M.Troeller
• visualization by: F.Loewner/M.Troeller
• SUN ULTRA1/170: 26 MB, 16,467 seconds
• AVS data: 534 MB
• Software: FEATFLOW1.0 + BOUSS

• For more details about numerical and algorithmic aspects see the `Mathematical Background' in the FEATFLOW manual or visit our paper archive for much more details.
• The problem-specific data for the applied software version including parameter files and input data can be downloaded here!