Computational Details:

"Flow around a wing construction at low Reynolds number"

• diameter of circle: 10
• length/height of (main) wing : 2.2/0.4
• inflow b.c.'s: normalized Dirichlet data (size 1) depending on the angle of attack.
• other b.c.'s: zero velocity at surface
• initial condition at t=0: starting from rest
• viscosity parameter: 1/nu=100

• coarse mesh (=level 1): 411 cells, 448 vertices, 2,131 d.o.f.'s
  

  
  
  

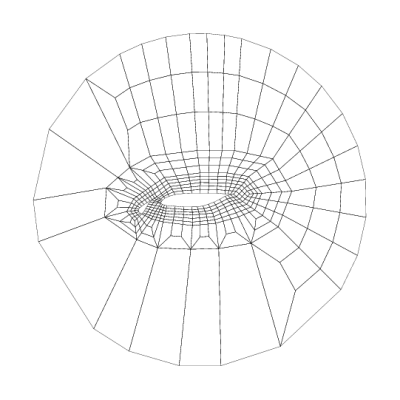
• uniform refinements with exact boundary adaption
• visualization on level 3: 6,576 cells, 6,727 vertices, 33,184 d.o.f.`s
• computational mesh on level 4: 26,304 cells, 26,607 vertices, 132,128 d.o.f.`s
• nonconforming nonparametric rotated bilinear fem's (meanvalue version), UPW

• equidistant time stepping for computation with k=0.066666667
• equidistant time stepping for visualization with k= 0.2 (= 1 frame)
• Total time T=50 seconds corresponds to 750 time steps
• fractional step theta scheme

• date: 01/20/98
• simulation by: S.Turek
• visualization by: L.Seioukova
• SUN ULTRA 45/250: 23 MB, 4,081 seconds
• AVS data: 385 MB
• Software: FEATFLOW1.0 + BOUSS

• For more details about numerical and algorithmic aspects see the `Mathematical Background' in the FEATFLOW manual or visit our paper archive for much more details.
• The problem-specific data for the applied software version including parameter files and input data can be downloaded here!