Hinweise zur Berechnung der Flächen unterhalb der Amalgamkurve.
Wir berechnen die quadratische Regressionskurve durch.
Hinweise zum Fit-Befehl finden Sie hier
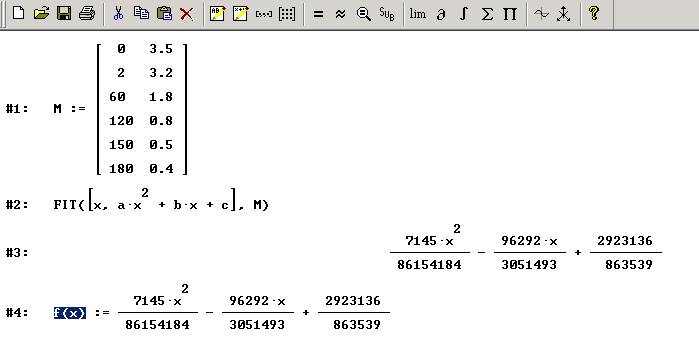
und definieren die Funktion f(x). Klicken Sie bitte nur f(x) an.
Nun berechnen wir mit dem Summenzeichen das Flächenmaß.
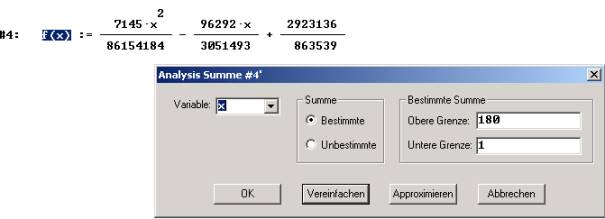
Mit Approximieren erhalten wir den Wert 257.8365956
Wir verbessern das Ergebnis durch Verkleinerung der Intervallbreiten. Wir zerlegen dazu das Intervall [0,180] in n gleichgroße Teile. Die Breite der Rechtecke ist demnach 180/n und die Höhe ist jeweils der linke Funktionswert im Teilintervall.
Die einzelnen Rechtecksflächen berechnen sich durch f(i*180/n)*(180/n).
Diesen Term geben wir in Derive ein.
Sie erhalten:
Durch SUB können Sie für n eine beliebige Zahl eingeben, oder durch lim den Grenzwert bestimmen.
Versuchen Sie es selbst. Klicken Sie dazu auf: eigener Versuch und schließen Sie abschließend das Derivefenster.