Einführung in die Integralrechnung
Amalgamfüllungen in Zähnen sind in den letzten Jahren sehr in Verruf geraten. Aus den Füllungen wird Quecksilber ausgeschieden und vom Körper aufgenommen. Um dieser Belastung zu entgehen, lassen sich manche Patienten die Amalgamfüllungen entfernen und durch Kunststofffüllungen oder Gold ersetzen.
Um einen Zusammenhang zwischen den Amalgamfüllungen und der Quecksilberbelastung belegen zu können, wurde bei einem Patienten über einen längeren Zeitraum die Quecksilberausscheidungen (hg in mg pro Tag ) gemessen. Es ergab sich folgendes Bild:
Quecksilberausscheidungen vor und nach der Entfernung von Amalgamfüllungen
|
Zeit in Tagen |
0 |
2 |
60 |
120 |
150 |
180 |
|
Hg in mg pro Tag |
3,5 |
3,2 |
1,8 |
0,8 |
0,5 |
0,4 |
Aufgabe:
Zeichnen Sie die Punkte in ein Koordinatensystem ein.
Hinweise zur Benutzung des Deriveprogramms finden sie unter Hinweise für die Zeichnung von Punkten
Sie können auch direkt eigener Versuch anklicken.
Schließen Sie bitte abschließend das Derivefenster.
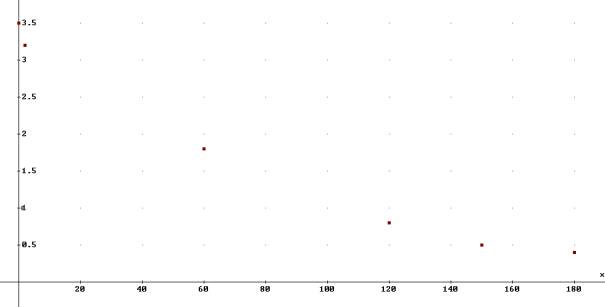
Um die ausgeschiedene Amalgammenge zu berechnen, verwenden wir Trapeze.
Die Flächeninhalte der Trapeze können mit Hand, Derive , Excel oder TI92 berechnet werden.
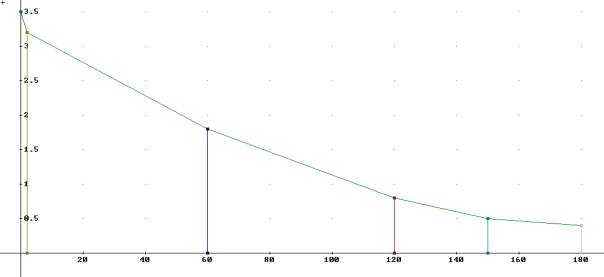
Aufgabe:
Führen Sie die Berechnung der Trapezflächen mit Derive
durch:
Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derivefenster.
Das Ergebnis der Flächenberechnung lautet: 262,7
Wir wollen das Ergebnis verbessern und suchen dazu einen Funktionsgraphen, der die Punkte möglichst gut approximiert
Es bieten sich verschiedene Funktionen an, auf deren Graphen die Punkte liegen.
Mit Derive kann man mehrere Lösungsideen realisieren
- Wir suchen eine Regressionskurve. Der Fit-Befehl berechnet solche Funktionsterme. Die Kurven haben zu den vorgegebenen Punkten den kleinsten quadratischen Abstand.
- Wir wählen eine bestimmte Anzahl von Punkten aus und legen eine entsprechende Polynomfunktion durch diese Punkte. Die Berechnung erfolgt über ein Gleichungssystem
Hinweise zur Berechnung von Polynomfunktionen
Versuch mit einer quadratischen Funktion
Ohne den Fit-Befehl nimmt man z.B. die Punkte (0/3.5), (60/1.8) und (180/0.4) und berechnet mit diesen die quadratische Funktion, die durch dieses drei Punkte verläuft.
Aufgabe :
Berechnen Sie die quadratische Funktion, die durch die angegebenen
Punkte verläuft.
Bearbeiten Sie die Hinweise zur Berechnung von Polynomfunktionen.
Sie können auch direkt eigener Versuch anklicken und die Aufgabe lösen.
Schließen Sie bitte abschließend das Derivefenster.
Versuch mit einer quadratischen Regression.
Aufgabe :
Berechnen Sie die quadratische Regressionskurve zu den vorgegebenen Punkten.
Bearbeiten Sie die Hinweise zum Fitbefehl
Sie können auch direkt eigener Versuch anklicken und die Aufgabe lösen.
Schließen Sie bitte abschließend das Derivefenster.
Aufgabe :
Berechnen Sie eine Regressionskurve höheren Grades zu den vorgegebenen Punkten.
Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derivefenster.
Die Lösung mit der quadratischen Regression hat folgendes Aussehen:
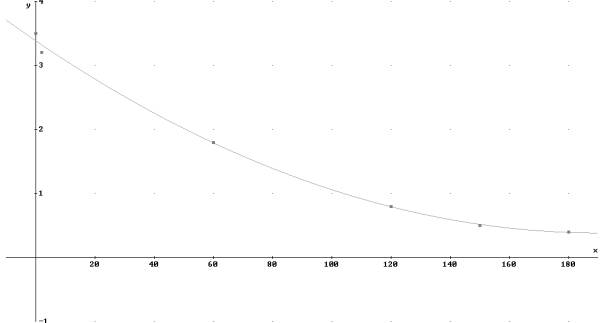
Mit Hilfe dieser oder ähnlicher Regressionskurven sind wir nun in der Lage, die Fläche genauer zu bestimmen
Wir summieren die Funktionswerte f(x) für alle natürlichen Zahlen von 1 bis 180 auf (wir bilden Rechtecke mit der Breite 1. Die Länge entspricht dem Funktionswert an der rechten Seite)
![]()
![]()
Die Genauigkeit der Berechnung kann durch Verkleinerung der Breite verbessert werden.
Halbieren wir die Breite der
Rechtecke, so erhalten wir doppelt so viele Rechtecke. Und jedes einzelne ist
berechenbar durch die Formel ![]() wobei mit i die
Rechtecke durchgezählt werden
wobei mit i die
Rechtecke durchgezählt werden
anschließend lässt man n gegen unendlich laufen (man setzt große Werte für n ein) und erhält einen guten Wert für das gesuchte Flächemaß.
Aufgabe :
Berechnen Sie den Flächeninhalt nach der vorgestellten Methode.
Bearbeiten Sie dazu die Hinweise zur Berechnung der Fläche unterhalb der Amalgamkurve
Sie können auch direkt eigener Versuch anklicken und die Aufgabe lösen.
Schließen Sie bitte abschließend das Derivefenster.
Gleiches kann man mit Rechtecken der Breite 1 und dem Funktionswert an der rechten Seite oder mit Trapezen durchführen. Lässt man auch hier n gegen unendlich laufen, so ergibt sich das gleiche Flächenmaß.
Aufgabe :
Berechnen Sie den Flächeninhalt nach den vorgestellten
Methode.
Klicken Sie dazu auf eigener Versuch und schließen Sie abschließend das Derievfenster.
Alle weiteren Versuche mit anderen möglichen Funktionen ergeben ähnliche Bilder, deren Güte man mit den Schülerinnen und Schülern diskutieren sollte auch in Hinblick auf Prognosen für die weitere Quecksilberausscheidungen.
Aufgabe :
Berechnen Sie den Flächeninhalt nach den vorgestellten
Methode mit anderen möglichen (Regressions-)funktionen.
Klicken Sie dazu auf eigener Versuch
und schließen Sie abschließend das Derievfenster.
Damit ist die Aufgabenstellung gelöst.