Computation of stress point value (Prandtl-Reuss model)

Finally, we show the results of a computation of the stress value 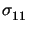 $\sigma_{11}^{}$(b)  at point  b  (see Figure 3) based on the nonstationary Prandtl-Reuss model. The algorithm used is that described in Section 3.2. The point  b  has been chosen for evaluating the stress since the elastic-plastic transition front passes over this point in the course of the loading process. This should result in a behaviour for the Prandtl-Reuss model different from that for the stationary Hencky model. The results indicate that our error estimation strategy also works within an incremental loading process for approximating the Prandtl-Reuss model. More detailed results and comparisons against other error estimators will be presented in [34].

Abbildung: 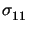$\sigma_{11}^{}$ : Time-dependent error behaviour in computing 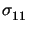 $\sigma_{11}^{}$(b)  for  k_n = 0.1, 0.2, 0.4, 0.8  on varying meshes with  N_max $\approx$ 4000  cells