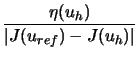Nächste Seite: Computation of contour integrals
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: Mesh refinement strategy
We have applied our technique for a posteriori error estimation to a proto-typical
test problem in plasticity which has already been considered in [31] in the
context of linear elasticity. Another application to a benchmark problem
in perfect plasticity will be presented in [33]. Our test case is the plane strain
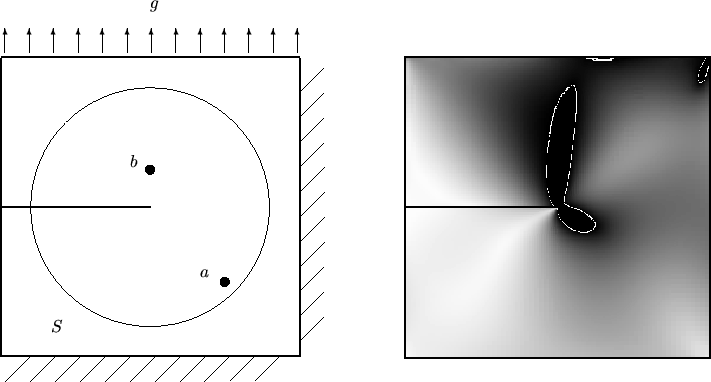
model of a square elastic disc with a crack subjected
to a growing (constant) boundary traction acting along the upper boundary
(see Figure 3).
Along the right-hand side and the lower boundary the body is
fixed and the remaining part of the boundary (including the crack) is left free.
This problem is interesting as its solution develops a singularity at the tip of
the crack where in the elastic case a stress concentration occurs with an asymptotic
behaviour (expressed in terms of polar coordinates) of the form
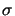
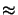 r-1/2 . Hence, local plastification will occur right form the
beginning of the loading process.
r-1/2 . Hence, local plastification will occur right form the
beginning of the loading process.
We consider the case of the linear isotropic material law in the form
and the perfect plastic behaviour is determined by the flow function
The values for the above parameters are set to
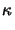 = 164206 , = 164206 , 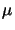 = 80193.80 , = 80193.80 , 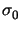 = 450 , = 450 , |
|
which corresponds to the properties of Aluminum (cf. [13]).
The boundary traction is assumed in the form
g = tg0 , with
g0 = 100 and t > 0 . In the case of the Hencky model, we take
tlim = 2.234 , since already for t = 2.3 , plastic collapse occurs.
Abbildung:
Geometry of the square disc test problem and plot
of
|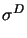 | (plastic regions black) computed on a mesh with
N
| (plastic regions black) computed on a mesh with
N 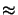 64, 000
cells
64, 000
cells
|
|
From the engineering point of view it is most interesting to
know the corresponding stress intensity factor which can be expressed in terms
of the (unknown) displacement u by evaluating contour integrals of the form
(see [15] and the literature cited therein)
Ju(u) = 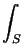 u . u . 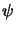 ds J ds J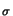 (u) = (u) = 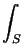 n . n .  (u) . (u) . 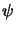 ds , ds , |
(50) |
where S is a suitable circular path around the tip of the crack,
and
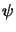 (
(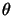 ) are certain trigonometric polynomials. These integrals are usually
generated numerically from a computed solution uh .
The question is now, what is the most economical mesh to compute Ju(u) and
J
) are certain trigonometric polynomials. These integrals are usually
generated numerically from a computed solution uh .
The question is now, what is the most economical mesh to compute Ju(u) and
J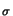 (u)
to best accuracy.
The traditional answer, based on a priori error
analysis, is that one should use a mesh which is optimal for the energy error. This
requires a graded refinement towards the corner point of the form
h(r)
(u)
to best accuracy.
The traditional answer, based on a priori error
analysis, is that one should use a mesh which is optimal for the energy error. This
requires a graded refinement towards the corner point of the form
h(r) 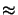 rh . However, this asymptotic information does not provide a useful error
bound on the meshes actually used. A further complication arises from
the weak stress singularity occurring at the point of discontinuity of the boundary
condition at the upper right corner. In such a situation when several accuracy
limiting effects occur simultaneously mere asymptotic error analysis will hardly lead to
reliable error bounds. Here, our new approach offers the possibility of rigorous
error control.
In order to demonstrate the local features of this technique, we also consider the
computation of the stress point-value
rh . However, this asymptotic information does not provide a useful error
bound on the meshes actually used. A further complication arises from
the weak stress singularity occurring at the point of discontinuity of the boundary
condition at the upper right corner. In such a situation when several accuracy
limiting effects occur simultaneously mere asymptotic error analysis will hardly lead to
reliable error bounds. Here, our new approach offers the possibility of rigorous
error control.
In order to demonstrate the local features of this technique, we also consider the
computation of the stress point-value
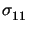 (a) (see Figure 3).
(a) (see Figure 3).
Finally, we apply the nonstationary Prandtl-Reuss model for the computation of the
stress point-value
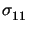 (b) (see Figure 3).
This demonstrates that, at least on a heuristic basis,
our approach also works within a incremental loading process. Further applications based
on the Prandtl-Reuss model will be presented in [34].
(b) (see Figure 3).
This demonstrates that, at least on a heuristic basis,
our approach also works within a incremental loading process. Further applications based
on the Prandtl-Reuss model will be presented in [34].
The solutions on very fine (adaptive) meshes with about 200,000 cells are taken as
reference solutions
uref for determining the relative errors
Erel : = | J(uh) - J(uref)|/| J(uref)|
on coarser meshes, while
Ratio : =
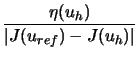
are the overestimation factors of the different error estimators. For mesh refinement
(and coarsening) we use the strategy described above.
Unterabschnitte



Nächste Seite: Computation of contour integrals
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: Mesh refinement strategy
sutti
2000-04-19
![]() (b) (see Figure 3).
This demonstrates that, at least on a heuristic basis,
our approach also works within a incremental loading process. Further applications based
on the Prandtl-Reuss model will be presented in [34].
(b) (see Figure 3).
This demonstrates that, at least on a heuristic basis,
our approach also works within a incremental loading process. Further applications based
on the Prandtl-Reuss model will be presented in [34].