


Nächste Seite: The new adaptive finite
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: The new approach for
The Prandtl-Reuss and Hencky model in perfect plasticity
The Prandtl-Reuss model in the theory of linear-elastic perfect plastic
material in classical notation reads (cf. [14] and [7])
div = - f, = - f,  ( ( ) = A ) = A + + 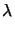 in in  , , |
(25) |
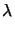 : ( : ( - -  ) ) 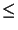 0 0   , with , with 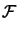 ( ( ) ) 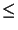 0, a.e. in 0, a.e. in , , 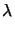 : :  = 0 in = 0 in  , , |
(26) |
 = 0 on = 0 on 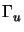 , ,  . n = g on . n = g on  . . |
(27) |
This set of equations describes the deformation of an elasto-plastic
body occupying a bounded domain
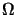
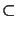
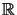 d (
d = 2 or 3) which is fixed along a part
d (
d = 2 or 3) which is fixed along a part
 of its boundary
of its boundary
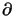
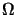 , under the action of a body force with density f
and a surface traction g along
, under the action of a body force with density f
and a surface traction g along
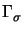 =
= 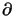
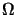

 . Here, u denotes the displacement,
. Here, u denotes the displacement,
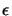 (u) =
(u) = 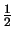 (
( u +
u +  uT) the strain- and
uT) the strain- and 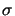 the stress-tensor. A is the material tensor
which is assumed to be symmetric and positive definite with inverse
C = A-1.
In addition, the plastic growth
is denoted by
the stress-tensor. A is the material tensor
which is assumed to be symmetric and positive definite with inverse
C = A-1.
In addition, the plastic growth
is denoted by  , and
, and 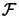 represents the continuous convex flow function
defined by the von Mises yield function
for some
represents the continuous convex flow function
defined by the von Mises yield function
for some
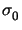 > 0 , depending on the deviatoric part of the stress tensor,
> 0 , depending on the deviatoric part of the stress tensor,
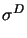 : =
: = 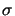 -
- 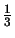 tr(
tr(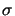 )I.
We consider the case of a quasi-static process, i.e., acceleration effects are neglected.
)I.
We consider the case of a quasi-static process, i.e., acceleration effects are neglected.
For applying a finite element method we have to
reformulate problem (23) in a variational setting.
Typically the behaviour of plastic material is a time dependent
process on a time interval
I : = [0, T] parametrizing the growing loading, i.e.,
the load functions are given in the form
f = f (t) = tf0 , g = g(t) = tg0 ,
with some prescribed load distributions
f0(x)
and
g0(x) .
In order to give the variational formulation, we use the function spaces
L2( )d : = L2( )d : = L2( , ,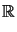 d), L2( d), L2( )d x dsym : = L2( )d x dsym : = L2( , ,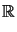 symd x d), symd x d), |
|
Hdiv = {  L2( L2( )d x dsym , div )d x dsym , div  L2( L2( )d} , )d} , |
|
and the sets of admissible stresses
| Hdivf, g |
= {  Hdiv, - div Hdiv, - div = f in = f in  , ,  . n = g on . n = g on  } , } , |
|
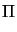 ( ( ) ) |
= {   , , 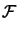 ( ( ) ) 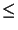 0a.e.in 0a.e.in } , } , |
|
for any appropriate function space
 .
Furthermore, we introduce the velocities of the displacement,
v =
.
Furthermore, we introduce the velocities of the displacement,
v = 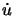 . We assume
the process to start with a stress free state, i.e.,
. We assume
the process to start with a stress free state, i.e.,
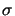 (0) = 0.
Using this notation the dual-mixed formulation
seeks a pair
{v,
(0) = 0.
Using this notation the dual-mixed formulation
seeks a pair
{v,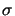 } : I
} : I L2(
L2(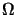 )d x
)d x 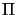 Hdiv * , g,
such that
Hdiv * , g,
such that
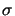 (0) = 0, and
(0) = 0, and
(A , , - -  ) + (v, div ) + (v, div - div - div ) ) 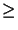 0 0    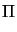 Hdiv * , 0 , Hdiv * , 0 , |
(28) |
- (div , , ) = (f, ) = (f, ) )    L2( L2( )d . )d . |
(29) |
Integrating in (24) by parts, we obtain the primal-mixed
variational formulation, where a pair
{v,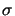 } : I
} : I V x
V x 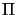 L2(
L2(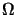 )d x dsym is sought
such that
)d x dsym is sought
such that
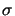 (0) = 0, and
(0) = 0, and
(A , , - -  ) - ( ) - ( (v), (v), - -  ) ) 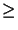 0 0    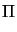 L2( L2( )d x dsym , )d x dsym , |
(30) |
( , , ( ( )) = (f, )) = (f, ) + (g, ) + (g, ) )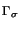    V . V . |
(31) |
Our computations for the elasto-plasticity problem are all based on this primal-mixed
formulation.
If the rate dependence in the plastic law in (23),
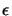 (
(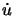 ) = A
) = A +
+  ,
is neglected, we arrive at the Hencky model of (stationary)
perfect plasticity (see, e.g., [7]). For this the primal-mixed variational
formulation reads
,
is neglected, we arrive at the Hencky model of (stationary)
perfect plasticity (see, e.g., [7]). For this the primal-mixed variational
formulation reads
(A , , - -  ) - ( ) - ( (u), (u), - -  ) ) 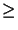 0 0    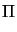 L2( L2( )d x dsym , )d x dsym , |
(32) |
( , , ( ( )) = (f, )) = (f, ) + (g, ) + (g, ) )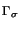    V . V . |
(33) |
The adventage of this formulation is that it can again be rewritten as a nonlinear
variational equation analogously as for the Strang model problem,
(C( (u)), (u)), ( ( )) : = ( )) : = (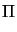 C C (u), (u), ( ( )) = (f, )) = (f, ) + (g, ) + (g, ) )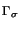    V , V , |
(34) |
where
Splitting the continuous loading process
f (t) , g(t) in the Prandtl-Reuss model
into a sequence of incremental load steps,
fn = fn - 1 + knf0 , gn = gn - 1 + kng0 ,
with a pseudo-time step length
kn : = tn - tn - 1, we obtain a sequence of Hencky-type problems,
(A , , - -  ) - (A ) - (A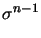 + kn + kn (vn), (vn), - -  ) ) 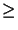 0 0    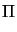 L2( L2( )d x dsym , )d x dsym , |
(36) |
( , , ( ( )) = (fn, )) = (fn, ) + (gn, ) + (gn, ) )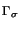    V , V , |
(37) |
with the initial value
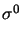 = 0.
According to the above discussion, each such load step is equivalent to a
nonlinear problem of the form
= 0.
According to the above discussion, each such load step is equivalent to a
nonlinear problem of the form
(C( (vn)), (vn)), ( ( )) : = ( )) : = (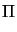 ( (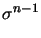 + knC + knC (vn)), (vn)), ( ( )) = (fn, )) = (fn, ) + (gn, ) + (gn, ) )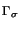    V . V . |
(38) |
Solving this equation gives us an update for the deformation velocity
vn 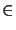 V and
then the new stress and deformation as
V and
then the new stress and deformation as

: =
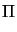
(
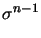
+
knC
(
vn))

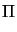 L2
L2(

)
d x dsym ,
un : =
un - 1 +
knvn  V
V .
This process is equivalent to applying the backward Euler time-stepping scheme to the
nonstationary problem (25). We will assume that the incremental
step
knf0 , kng0 is chosen small enough that the resulting time-discretization
error can be neglected compared to the error resulting from the finite element
approximation. Our numerical tests show that this is realistic, at least for the
type of problems considered. The stationary Hencky model (26) may
be viewed as the approximation of the Prandtl-Reuss model by one time step of length
k = 1 starting form the initial state
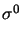
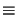 0 , u0
0 , u0 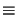 0.
0.
Finally, the nonlinear problems (30) are
approximated
by a damped Newton iteration. Starting from the result at the preceding load level,
vn, 0 : = vn - 1, the iteration step
vn, i - 1 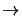 vn, i reads
vn, i reads
(C'( (vn, i - 1)) (vn, i - 1)) ( ( vn, i), vn, i), ( ( )) = (fn, )) = (fn, ) + (gn, ) + (gn, ) )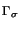 - (C( - (C( (vn, i - 1), (vn, i - 1), ( ( )) ))    V , V , |
(39) |
with the Jacobian
C'( . ) of the function
C( . ) , followed by the
update
vn, i =
vn, i - 1 +
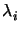
 vn, i
vn, i .
The damping parameter
0 < 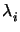
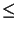 1 is determined in the form
1 is determined in the form
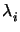 = 2-r such that the residual norm is decreased.
Hence, we have reduced the nonlinear plasticity problem (23)
on the continuous level to a sequence of linear problems of the form
= 2-r such that the residual norm is decreased.
Hence, we have reduced the nonlinear plasticity problem (23)
on the continuous level to a sequence of linear problems of the form
(C'( (v)) (v)) (w), (w), ( ( )) = l ( )) = l ( ) )    V , V , |
(40) |
with certain functionals
l ( . ) defined on V.
These may be solved by the CR-method with multigrid acceleration.
The use of multigrid is rather natural as in the course of the mesh refinement
process a sequence of nested meshes is automatically generated. Since the emphasis
of this paper is on the aspect of a posteriori error estimation and mesh design,
we do not go here into the details of the algebraic solution techniques and instead
refer to [33] and [34]. Again the error estimation uses the general
approach described above applied to the nonlinear problem
(30), i.e., the meshes are kept fixed during
the Newton iteration, but are dynamically adapted in the coarse of the time stepping.
The corresponding linearized dual problems
(C'( (uh) (uh) ( ( ), ), (zh)) = J( (zh)) = J( ) )    Vh . Vh . |
(41) |
are solved by the same technique as used for solving the Newton steps
(31).
We remark that, in contrast to really time dependent problems involving
acceleration terms, the control of the time-stepping error in the quasi-stationary
Prandtl-Reuss model is less critical. Since in each incremental load step the
deformation velocity
vn =  is updated, we do not expect much
accumulation of these local errors over the loading path. Hence it seems justified to
estimate the global spatial error in this process by simply treating it as a sequence
of stationary problems. This approach, of course, would be disastrous in the case of
a parabolic problem like, e.g., the heat equation.
is updated, we do not expect much
accumulation of these local errors over the loading path. Hence it seems justified to
estimate the global spatial error in this process by simply treating it as a sequence
of stationary problems. This approach, of course, would be disastrous in the case of
a parabolic problem like, e.g., the heat equation.



Nächste Seite: The new adaptive finite
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: The new approach for
sutti
2000-04-19
![]() (
(![]() ) = A
) = A![]() +
+ ![]() ,
is neglected, we arrive at the Hencky model of (stationary)
perfect plasticity (see, e.g., [7]). For this the primal-mixed variational
formulation reads
,
is neglected, we arrive at the Hencky model of (stationary)
perfect plasticity (see, e.g., [7]). For this the primal-mixed variational
formulation reads

![]()
![]() 0 , u0
0 , u0 ![]() 0.
0.
![]() vn, i reads
vn, i reads
![]() is updated, we do not expect much
accumulation of these local errors over the loading path. Hence it seems justified to
estimate the global spatial error in this process by simply treating it as a sequence
of stationary problems. This approach, of course, would be disastrous in the case of
a parabolic problem like, e.g., the heat equation.
is updated, we do not expect much
accumulation of these local errors over the loading path. Hence it seems justified to
estimate the global spatial error in this process by simply treating it as a sequence
of stationary problems. This approach, of course, would be disastrous in the case of
a parabolic problem like, e.g., the heat equation.