


Nächste Seite: Angewandte Methoden, Ergebnisse und
Aufwärts: plastiwww
Vorherige Seite: Zusammenfassung
The conventional strategies for mesh refinement in finite element methods are
mostly based on a posteriori error estimates in the global energy norm. Such
estimates reflect the approximation properties of the trial functions by local
interpolation constants while the stability property of the continuous model
enters through a global coercivity constant. However, meshes generated on the basis
of such global error estimates are not appropriate in computing local
quantities as, e.g., point values or contour integrals, and in the case of
nonlinear material behavior.
Recently a new technique for a posteriori error control and adaptive mesh design
for finite element methods has been proposed in [25], [26], and
[31]. Following the general approach of C. Johnson and his co-workers,
[11] and [4], residual-based a posteriori error
estimates are derived via duality arguments. Here, we carry this idea further
into a feed-back method in which the dual solutions are approximated on the
current meshes and used as local weights in the a posteriori error estimates
multiplying the residuals of the computed solution. In this way local information
about the mechanism of error propagation is captured which results in most economical
meshes as well as accurate error bounds in the course of a dynamic mesh adaptation
process. The additional work required by the computation of the weights is acceptable
as it usually amounts to less than 30% of the total cost.
This approach has been presented in [31] for primal as well as
dual-mixed finite element methods in linear elasticity. Here, it is developed
further for solving finite element models of Hencky- and Prandtl-Reuss-type in
linear-elastic perfect plasticity. We concentrate
on the primal-mixed formulation as in this case the yield-constraint can be
incorporated into a nonlinear material law which reduces the linear variational
inequality to a nonlinear variational equation and allows for the use of
efficient solution methods. In the dual-mixed formulation the pointwise
constraints have to be explicitly satisfied by the stresses which
makes the solution of the resulting algebraic problems much harder.
We recall the basic concept of our method for a posteriori
error estimation at a simple model problem due to Strang [18].
The physical problem is that of an infinitely long straight pipe, with
quadratic cross-section
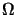
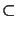
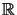 2 , filled with
plastic material adherent to the walls and subjected to a volume force f
acting in vertical direction (see Figure 1).
The mathematical model seeks a scalar displacement u in the vertical
direction and a stress vector
2 , filled with
plastic material adherent to the walls and subjected to a volume force f
acting in vertical direction (see Figure 1).
The mathematical model seeks a scalar displacement u in the vertical
direction and a stress vector
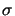 = (
= (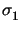 ,
,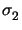 )
as functions on
)
as functions on
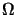 . The plastic behaviour of the material
is taken into account by the nonlinear restriction
|
. The plastic behaviour of the material
is taken into account by the nonlinear restriction
|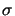 |
| 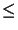 1 .
This results in the system
1 .
This results in the system
-div = f , = f ,  = = 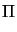  u in u in  , u = 0 on , u = 0 on   , , |
(1) |
where 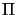 denotes the pointwise projection onto the unit circle. For the
moment, let
us assume that the stresses are small, so that the side condition can be
neglected leading to essentially elastic behaviour. Then, (1)
reduces to the linear boundary value problem
denotes the pointwise projection onto the unit circle. For the
moment, let
us assume that the stresses are small, so that the side condition can be
neglected leading to essentially elastic behaviour. Then, (1)
reduces to the linear boundary value problem
- 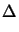 u = f in u = f in  , u = 0 on , u = 0 on   . . |
(2) |
Abbildung 1:
Geometry sketch of the Strang example
 |
We discretise this problem by a
conforming finite element method using piecewise linear or (isoparametricly)
bilinear shape functions on triangular or
quadrilateral meshes
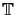 h = {K}, respectively, satisfying the usual condition
of shape regularity
(cf. [2]). For ease of mesh refinement and coarsening hanging nodes
are allowed in our implementation.
The width of the mesh
h = {K}, respectively, satisfying the usual condition
of shape regularity
(cf. [2]). For ease of mesh refinement and coarsening hanging nodes
are allowed in our implementation.
The width of the mesh
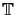 h is characterised in terms of the piecewise constant
mesh size function
h = h(x), 0 < h
h is characterised in terms of the piecewise constant
mesh size function
h = h(x), 0 < h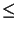 1, where
hK : = h| K = diam(K) and
hmax =
1, where
hK : = h| K = diam(K) and
hmax = 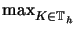 hK.
Using the notation
Vh
hK.
Using the notation
Vh 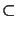 V = H10(
V = H10(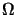 ) for the corresponding finite element
subspaces, the approximate solution
uh
) for the corresponding finite element
subspaces, the approximate solution
uh 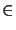 Vh is determined by the discrete
equation
Vh is determined by the discrete
equation
Here and below,
( . , . ) denotes
the inner product of
L2(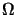 ) and | . |
the corresponding norm, while
(
) and | . |
the corresponding norm, while
( . ,
. , . ) is the natural
energy inner product of problem (2). Further,
Hm(
. ) is the natural
energy inner product of problem (2). Further,
Hm(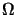 ),
for
m
),
for
m 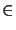
 , denotes the
usual m-th order Sobolev space with norm
| . |m, and
H10(
, denotes the
usual m-th order Sobolev space with norm
| . |m, and
H10(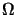 ) the
subset of
H1(
) the
subset of
H1(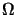 ) of functions vanishing on
) of functions vanishing on
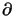
 . These are
all spaces of either scalar or vector-valued functions and no distinction
will be made in the notation of the corresponding inner products and norms.
. These are
all spaces of either scalar or vector-valued functions and no distinction
will be made in the notation of the corresponding inner products and norms.
In [26] a new concept has been proposed for estimating the
error in the scheme (3) for general error measures
given in terms of linear functionals J( . ) defined on
the space V, or on a suitable subspace containing the finite element space
Vh and the exact solution u. Relevant examples are torsion moments,
stress values, or the mean surface tension,
J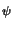 (u) = (u) =  u u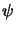 dx , Jij(u) = dx , Jij(u) = 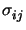 (u)(x0) , J (u)(x0) , J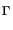 (u) = (u) =  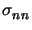 (u) ds . (u) ds . |
|
Then, following a common strategy for residual-based a posteriori error
estimation (see [11], [21], [4], and [26]),
we utilize the solution
z 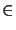 V of the corresponding dual problem
V of the corresponding dual problem
to derive a representation of the error e = u - uh,
J(e) = ( e, e, z) . z) . |
(5) |
Further, using the Galerkin orthogonality relation
( e,
e,
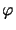 h) = 0 ,
h) = 0 , 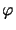
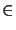 Vh, and element-wise integration by parts, it follows that
Vh, and element-wise integration by parts, it follows that
J(e) =  ![$\displaystyle \left\{\vphantom{(f+\Delta u_h,z-z_h)_K - \tfrac{1}{2} ([\partial_nu_h],z-z_h)_{\partial K} }\right.$](img41.gif) (f + (f + 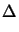 uh, z - zh)K - uh, z - zh)K - 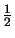 ([ ([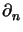 uh], z - zh) uh], z - zh)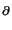 K K![$\displaystyle \left.\vphantom{(f+\Delta u_h,z-z_h)_K - \tfrac{1}{2} ([\partial_nu_h],z-z_h)_{\partial K} }\right\}$](img45.gif) , , |
(6) |
where
[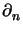 uh] denotes the jump of the normal derivative
uh] denotes the jump of the normal derivative
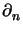 uh accross the interelement boundaries.
From (6), we deduce the a posteriori error bound
uh accross the interelement boundaries.
From (6), we deduce the a posteriori error bound
with the local residuals 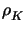 and weights
and weights 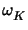 defined by
defined by
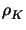 |
: = hK| f + 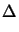 uh|K + uh|K + 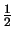 hK1/2| n . [ hK1/2| n . [ uh]| uh]|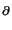 K , K , |
|
 |
: = max hK-1| z - zh|K, hK-1/2| z - zh| hK-1| z - zh|K, hK-1/2| z - zh|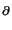 K K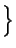 . . |
|
Weighted a posteriori error estimates in global norms as the energy norm
or the L2 norm can obtained within this framework by taking the special error
functionals
JE( ) = | ) = | e|-1 e|-1   . .  e dx , JL2( e dx , JL2( ) = | e|-1 ) = | e|-1  e dx , e dx , |
(8) |
which depend on the error e itself. In this case, the evaluation of
the weight factors
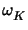 , i.e., the computation of the dual solution
z , requires to approximate the functional
J( . ) . This
may be achieved by replacing the unknown error e by some approximation
, i.e., the computation of the dual solution
z , requires to approximate the functional
J( . ) . This
may be achieved by replacing the unknown error e by some approximation
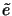 =
= 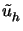 - uh obtained by extrapolation from two consecutively
coarser meshes.
- uh obtained by extrapolation from two consecutively
coarser meshes.
In general, the weights
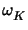 cannot be determined analytically, but have
to be computed by solving the dual problem numerically on the available mesh. To this
end one uses the interpolation estimate
cannot be determined analytically, but have
to be computed by solving the dual problem numerically on the available mesh. To this
end one uses the interpolation estimate
for
z 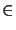 H2(K), and evaluates the right hand side by simply taking second order
difference quotients of the approximate dual solution
H2(K), and evaluates the right hand side by simply taking second order
difference quotients of the approximate dual solution
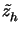
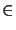 Vh,
Vh,
where xK is the mid-point of element K. This results in approximate
a posteriori error bounds
It has been demonstrated in [26] that this approximation has only minor
effects on the quality of the resulting meshes.
The interpolation constant Ci may be set equal to one. In our test
calculations, we actually set it to
Ci = 0.2 , in order to compensate for the overestimation effect in the
resulting approximate a posteriori estimate.
The a posteriori error estimate (11) provides the basis
of a feed-back process by which optimally refined meshes can be generated. On the current
mesh the dual solution is computed numerically yielding approximate weights. Using the
resulting a posteriori error estimate the mesh is refined according, for example, to
the strategy described below. This process is repeated yielding more and more accurate
weights, i.e., a posteriori error estimates, until the prescribed stopping criterion is
fulfilled. This approach allows us to construct almost optimal meshes for various
kinds of error measures, where ,,optimal'' can mean ,,most economical for
achieving a prescribed accuracy TOL'' or ,,most accurate for a given maximum
number Nmax of mesh points''.
The outlined approach to error control for finite element Galerkin schemes by weighted
a posteriori error estimates is rather universal as it can, in principle,
be applied to almost any problem,
linear or nonlinear, which is posed in a variational setting. This has already been
demonstrated for simple linear model cases in [26], for the nonlinear
Navier-Stokes equations in fluid mechanics in [25], for ordinary differential
equations in [27], for one-dimensional combustion problems in [28],
for integro-differential equations modelling radiative transfer in astrophysics in
[30], and for problemes in linear elasticity in [31].



Nächste Seite: Angewandte Methoden, Ergebnisse und
Aufwärts: plastiwww
Vorherige Seite: Zusammenfassung
sutti
2000-04-19
![]()
![]()
![]() 2 , filled with
plastic material adherent to the walls and subjected to a volume force f
acting in vertical direction (see Figure 1).
The mathematical model seeks a scalar displacement u in the vertical
direction and a stress vector
2 , filled with
plastic material adherent to the walls and subjected to a volume force f
acting in vertical direction (see Figure 1).
The mathematical model seeks a scalar displacement u in the vertical
direction and a stress vector
![]() = (
= (![]() ,
,![]() )
as functions on
)
as functions on
![]() . The plastic behaviour of the material
is taken into account by the nonlinear restriction
|
. The plastic behaviour of the material
is taken into account by the nonlinear restriction
|![]() |
| ![]() 1 .
This results in the system
1 .
This results in the system
![]() cannot be determined analytically, but have
to be computed by solving the dual problem numerically on the available mesh. To this
end one uses the interpolation estimate
cannot be determined analytically, but have
to be computed by solving the dual problem numerically on the available mesh. To this
end one uses the interpolation estimate