


Nächste Seite: Numerical tests
Aufwärts: The new adaptive finite
Vorherige Seite: A posteriori error estimation
We describe the strategy used for local mesh refinement on the basis of the
error estimators introduced above.
By local averaging the values of the norm
|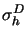 | of the stress deviator
are known in each vertex of the triangulation. We call a cell elastic,
if
|
| of the stress deviator
are known in each vertex of the triangulation. We call a cell elastic,
if
|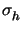 | <
| < 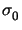 at each vertex, and plastic, if
|
at each vertex, and plastic, if
|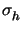 | =
| = 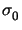 at each
vertex. The remaining cells represent the transition zone between elastic and plastic
behaviour.
at each
vertex. The remaining cells represent the transition zone between elastic and plastic
behaviour.
The mesh refinement process in each adaptive step is based on error bounds
of the form
Our goal is to minimize the degree of equidistribution 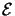 of the error indicators
of the error indicators
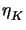 , i.e., the ratio of
, i.e., the ratio of
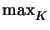 {
{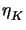 } and
} and
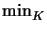 {
{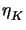 } ,
and, at the same time, to keep the total number of cells below a fixed (prescribed)
number
Nmax . To this end, we use the following strategy:
} ,
and, at the same time, to keep the total number of cells below a fixed (prescribed)
number
Nmax . To this end, we use the following strategy:
Mesh adaptiation Strategy: The elements are ordered according to the
size 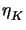 . A fixed portion (say 20%) of cells K with smallest contributions
. A fixed portion (say 20%) of cells K with smallest contributions
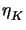 to the indicator value
to the indicator value 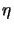 is marked to be deleted.
Then, we refine those cells with largest
is marked to be deleted.
Then, we refine those cells with largest 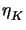 , so that the desired
number of cells
Nmax is almost reached.
, so that the desired
number of cells
Nmax is almost reached.



Nächste Seite: Numerical tests
Aufwärts: The new adaptive finite
Vorherige Seite: A posteriori error estimation
sutti
2000-04-19
![]() . A fixed portion (say 20%) of cells K with smallest contributions
. A fixed portion (say 20%) of cells K with smallest contributions
![]() to the indicator value
to the indicator value ![]() is marked to be deleted.
Then, we refine those cells with largest
is marked to be deleted.
Then, we refine those cells with largest ![]() , so that the desired
number of cells
Nmax is almost reached.
, so that the desired
number of cells
Nmax is almost reached.