Nächste Seite: The Prandtl-Reuss and Hencky
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: Angewandte Methoden, Ergebnisse und
The approach to adaptive error control in finite element methods described above
can easily be extended to nonlinear situations.
We illustrate this for the Strang problem introduced above.
The dual-mixed variational formulation of (1) reads
( , , - -  ) + (v, div ) + (v, div - div - div ) )  0 0     Hdiv , Hdiv , |
(12) |
- (div , , ) = (f, ) = (f, ) )    L2( L2( ) , ) , |
(13) |
where
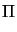 Hdiv
Hdiv = {

 L2
L2(

)
2 , div

 L2
L2(

), |

|
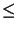
1 a.e. in

} .
Integrating in (12) by parts, we obtain the primal-mixed
formulation
( , , - -  ) - ( ) - ( v, v, - -  ) ) 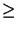 0 0    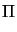 L2( L2( )2 , )2 , |
(14) |
( , ,  ) = (f, ) = (f, ) )    V , V , |
(15) |
where
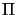 L2(
L2(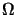 )2 has the obvious meaning.
Although, the primal-mixed formulation is not properly posed, as it requires more
regularity for the deformation,
u
)2 has the obvious meaning.
Although, the primal-mixed formulation is not properly posed, as it requires more
regularity for the deformation,
u 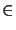 H1(
H1(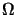 ), than what can be expected in general,
it has a feature which makes it particular attractive as starting point for the numerical
approximation. The first relation in (13) can equivalently
be written in the form
), than what can be expected in general,
it has a feature which makes it particular attractive as starting point for the numerical
approximation. The first relation in (13) can equivalently
be written in the form
with the function
Feeding this into the second equation in (13),
we obtain the nonlinear variational equation
This problem is now discretized by the finite element method,
(C( uh), uh),  ) = (f, ) = (f, ) )    Vh . Vh . |
(19) |
Combining (16) and (17),
we obtain the nonlinear Galerkin orthogonality relation
(C( u) - C( u) - C( uh), uh),  ) = ) = 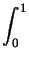 (C'( (C'( (su + (1 - s)uh)) (su + (1 - s)uh)) (u - uh), (u - uh),  ) ds = 0 , ) ds = 0 , |
(20) |
for
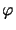
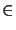 Vh , with the Jacobian
C'( . ) of the function
C( . ) , defined by
Vh , with the Jacobian
C'( . ) of the function
C( . ) , defined by
C'( ) : = ) : =  |
(21) |
Now, suppose that the quantity J(u) has to be computed. For representing the error
J(e) = J(u) - J(uh), we use the solution z of the linear dual problem
L(u, uh; , z) = J( , z) = J( ) )    V , V , |
(22) |
with the bilinear form
L(u, uh; , ,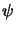 ) : = ) : = 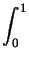 (C'( (C'( (su + (1 - s)uh)) (su + (1 - s)uh))  , , 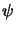 ) ds . ) ds . |
|
We assume that this dual solution is well defined. By the orthogonality relation
(18), there holds
J(e) = L(u, uh;e, z - zh) ,
with a suitable approximation
zh 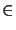 Vh.
Then, analogously as in the linear case, we obtain the error representation
Vh.
Then, analogously as in the linear case, we obtain the error representation
J(e) = 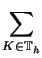 ![$\displaystyle \left\{\vphantom{(f-\div C(\nabla u_h),z-z_h)_K - \textstyle{\frac{1}{2}}(n\cdot [C(\nabla u_h)],z-z_h)_{\partial K} }\right.$](img70.gif) (f - divC( (f - divC( uh), z - zh)K - uh), z - zh)K - 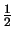 (n . [C( (n . [C( uh)], z - zh) uh)], z - zh)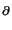 K K![$\displaystyle \left.\vphantom{(f-\div C(\nabla u_h),z-z_h)_K - \textstyle{\frac{1}{2}}(n\cdot [C(\nabla u_h)],z-z_h)_{\partial K} }\right\}$](img71.gif) . . |
|
From that, the following a posteriori error estimate follows,
with the local residuals and weights defined by
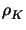 |
: = hK| f - divC( uh)|K + hK1/2| n . [C( uh)|K + hK1/2| n . [C( uh)]| uh)]|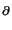 K , K , |
|
 |
: = max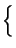 hK-1| z - zh|K, hK-1/2| z - zh| hK-1| z - zh|K, hK-1/2| z - zh|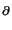 K K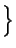 . . |
|
In order to evaluate these bounds, we replace the unknown solution u in the
bilinear form
L(u, uh; . , . ) by the currently computed approximation uh ,
and solve the corresponding perturbed dual problem by the same method as used in computing
uh , yielding an approximation
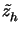
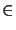 Vh to the exact dual solution z,
Vh to the exact dual solution z,
L(uh, uh; h, h,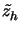 ) = J( ) = J( h) h)   h h  Vh . Vh . |
(24) |
The weights 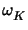 may then again be approximated as in the linear case described
above. We emphasize that the computation of the weights requires only to solve
linear problems and normally only amounts to a small fraction of the total cost
within a Newton iteration for the nonlinear problem.
may then again be approximated as in the linear case described
above. We emphasize that the computation of the weights requires only to solve
linear problems and normally only amounts to a small fraction of the total cost
within a Newton iteration for the nonlinear problem.



Nächste Seite: The Prandtl-Reuss and Hencky
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: Angewandte Methoden, Ergebnisse und
sutti
2000-04-19