


Nächste Seite: A posteriori error estimation
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: The Prandtl-Reuss and Hencky
Our numerical scheme for solving the Prandtl-Reuss model in perfect plasticity
(23) is based on the primal formulation
(30) within an incremental loading process.
In each load step a stationary Hencky-type problem is solved using an
adaptive finite element discretization. The finite element meshes are optimized
separately within each load step in accordance to the particular target functional
J( . ) leading to a dynamic development of refinement and coarsening
over the whole calculation cycle.
We recall the notation for this framework. The space of admissible deformations is
Let
Vh 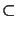 V be
finite element spaces as described above, i.e., the underlying meshes consisting of
triangles or quadrilaterals are shape-regular, but may contain hanging nodes,
and the shape functions are linear or (isoparametricly) bilinear.
Simplifying notation, the domain
V be
finite element spaces as described above, i.e., the underlying meshes consisting of
triangles or quadrilaterals are shape-regular, but may contain hanging nodes,
and the shape functions are linear or (isoparametricly) bilinear.
Simplifying notation, the domain 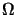 is assumed to be polyhedral in order
to ease the approximation of the boundary. More general situations may be treated by
the usual modifications.
is assumed to be polyhedral in order
to ease the approximation of the boundary. More general situations may be treated by
the usual modifications.
The loading process is started from the initial state
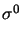
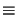 0.
In each load step
tn - 1
0.
In each load step
tn - 1 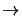 tn , the nonlinear problem
(30) has to be solved resulting in the following
equation for the discrete deformation velocity
vnh
tn , the nonlinear problem
(30) has to be solved resulting in the following
equation for the discrete deformation velocity
vnh 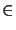 Vh,
Vh,
(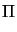 ( (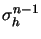 + knC + knC (vnh)), (vnh)), ( ( )) = (fn, )) = (fn, ) + (gn, ) + (gn, ) )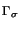    Vh . Vh . |
(42) |
From this, we obtain the stress update as
where the projection 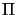 is as defined above. Further, starting from the
initial deformation
u0h
is as defined above. Further, starting from the
initial deformation
u0h 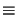 0, we obtain corresponding
approximate deformations as
0, we obtain corresponding
approximate deformations as
unh : = un - 1h + knvnh .
Hence, (34) may be rewritten as
(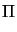 ( (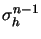 + C + C (unh - un - 1h)), (unh - un - 1h)), ( ( )) = (fn, )) = (fn, ) + (gn, ) + (gn, ) )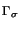    Vh . Vh . |
(44) |
From now on, we suppress the sub- and superscript n and consider
Hencky-type problems of the form
(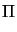 ( (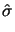 + C + C (uh - (uh - 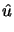 )), )), ( ( )) = (f, )) = (f, ) + (g, ) + (g, ) )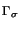    Vh , Vh , |
(45) |
with given initial stress
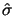 and deformation
and deformation
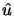 .
From (37),
we obtain deformations
uh
.
From (37),
we obtain deformations
uh 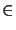 Vh and associated stresses
approximating the
solutions
u
Vh and associated stresses
approximating the
solutions
u 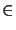 V and
V and
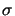
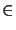
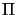 L2(
L2(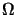 )d x dsym of the
corresponding continuous problem
)d x dsym of the
corresponding continuous problem
(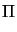 ( (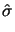 + C + C (u - (u - 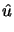 )), )), ( ( )) = (f, )) = (f, ) + (g, ) + (g, ) )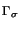    V . V . |
(46) |
Clearly, for
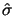 = 0 and
= 0 and
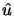 = 0, this reduces to the usual
Hencky model (27).
= 0, this reduces to the usual
Hencky model (27).
Unterabschnitte



Nächste Seite: A posteriori error estimation
Aufwärts: Angewandte Methoden, Ergebnisse und
Vorherige Seite: The Prandtl-Reuss and Hencky
sutti
2000-04-19
![]()
![]() 0.
In each load step
tn - 1
0.
In each load step
tn - 1 ![]() tn , the nonlinear problem
(30) has to be solved resulting in the following
equation for the discrete deformation velocity
vnh
tn , the nonlinear problem
(30) has to be solved resulting in the following
equation for the discrete deformation velocity
vnh ![]() Vh,
Vh,