DFG flow around cylinder benchmark 2D-1, laminar case (Re=20)
This benchmark simulates a fluid in a pipe with a circular obstacle. It is set up in 2D and simulated stationary.
Geometry and flow configuration
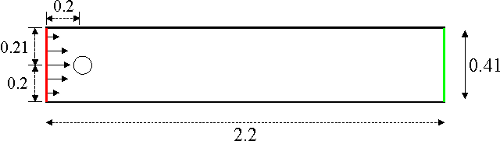
The underlying geometry is a pipe without a circular cylinder $\Omega=[0,2.2] \times [0,0.41] \setminus B_r(0.2,0.2)$ with $r=0.05$. Taking a fluid density of $\rho=1.0$, the fluid is characterised by the stationary Navier-Stokes equations
$$ -\nu\Delta u + u\nabla u + \nabla p = 0,\qquad \text{\div }u = 0 $$
with $u$ defining the velocity and $p$ the pressure. The kinematic viscosity is taken as
$$ \nu = 0.001. $$
Boundary conditions
For the lower and upper walls $\Gamma_1=[0,2.2]\times{0}$ and $\Gamma_1=[0,2.2]\times{0.41}$ as well as the boundary $S=\partial B_r(0.2,0.2)$, no-slip boundary conditions are defined,
$$ u_{|\Gamma_1} = u_{|\Gamma_3} = u_{|S} = 0. $$
On the left edge $\Gamma_4={0}\times[0,0.41]$, a parabolic inflow profile is prescribed,
$$ u(0,y) = \left( \frac{4 U y (0.41-y)}{0.41^2} , 0 \right), $$
with a maximum velocity $U=0.3$. On the right edge $\Gamma_4={2.2}\times[0,0.41]$, do-nothing boundary conditions define the outflow,
$$ \nu \partial_\eta u - p \eta = 0 $$
with $\eta$ denoting the outer normal vector.
Reynolds number
For a maximum velocity of $U=0.3$, the parabolic profile results in a mean velocity
$$ U_\text{mean} = \frac{2}{3}\cdot 0.3 = 0.2. $$
The characteristic length of the flow configuration is
$$ L = 2\cdot 0.05 = 0.1 $$
the diameter of the object perpendicular to the flow direction. This results in a Reynolds number
$$ \text{Re} = \frac{U_\text{mean} L}{\nu} = \frac{0.2 \cdot 0.1}{0.001} = 20. $$
For this Reynolds number, the flow turns into a stationary. This is visualised in the Figure below.
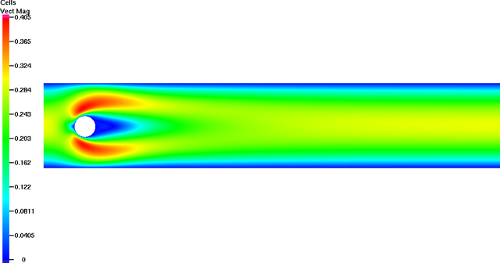
Velocity magnitude

Pressure

Streamfunction
Important numerical quantities
For the numerical comparison of data, the forces around the circle are measured. These drag and lift forces are defined by
$$ \begin{pmatrix} F_D F_L \end{pmatrix} = \int_{S} \sigma \eta ds $$
with $\eta$ denoting the outer normal vector of the circle. The stress tensor $\sigma$ in this formula is defined as
$$ \sigma := \nu \nabla u - p I. $$
A not so straightforward calculation which exploits $u_{|S}=0$ can be used to derive the following formulas for the drag and lift force, which can alternatively be used in 2D, see [3]:
$$ F_D = \int_S \left(\nu \frac{\partial u_{\tau}}{\partial_\eta} \eta_2 - p \eta_1 \right) ds,\quad F_L = - \int_S \left(\nu \frac{\partial u_{\tau}}{\partial_\eta} \eta_1 + p \eta_2 \right) ds $$
From the forces, one obtains the dimensionless drag and lift coefficients,
$$ C_D = \frac{2}{U_\text{mean}^2 L} F_D,\qquad C_L = \frac{2}{U_\text{mean}^2 L} F_L. $$
Setup of the test and data measurement
To measure numerical data, one carries out a stationary numerical simulation
The following numerical quantities are measured:
- The drag and lift coefficients $C_D$ and $C_L$.
- the pressure difference $p_\text{diff}:=p(a_1)-p(a_2)$ in the points $a_1=(0.15,0.2)$ and $a_2=(0.25,0.2)$ on the front and rear side of the cylinder.
Reference results
In [2], the results have been computed with high order spectral methods. The following values define the reference values for this test:
- Drag coefficient $$ C_D = 5.57953523384 $$
- Lift coefficient $$ C_L = 0.010618948146 $$
- Pressure difference $$ p_\text{diff} = 0.11752016697 $$
References
| Id | Title |
|---|---|
| [1] | Turek, Schaefer; Benchmark computations of laminar flow around cylinder; in Flow Simulation with High-Performance Computers II, Notes on Numerical Fluid Mechanics 52, 547-566, Vieweg 1996 |
| [2] | Nabh; On High Order Methods for the Stationary Incompressible Navier-Stokes Equations; University of Heidelberg; Preprint 42/98, 1998; Download |
| [3] | John; Higher order Finite element methods and multigrid solvers in a benchmark problem for the 3D Navier-Stokes equations, Int. J. Numer. Meth. Fluids 2002; 40: 775-798 (DOI: 10.1002/ d.377) |
